Multi-Scale Topology Optimization of Discrete Lattice Structures
1.583 Final Project
Amira Abdel-Rahman
PhD Student
Center for Bits and Atoms (CBA)

Background
Digital Material
Discrete set of parts with relative positions and orientations; where global geometry is determined from local constraints, reversibly join parts with dissimilar properties to build heterogeneous functional systems.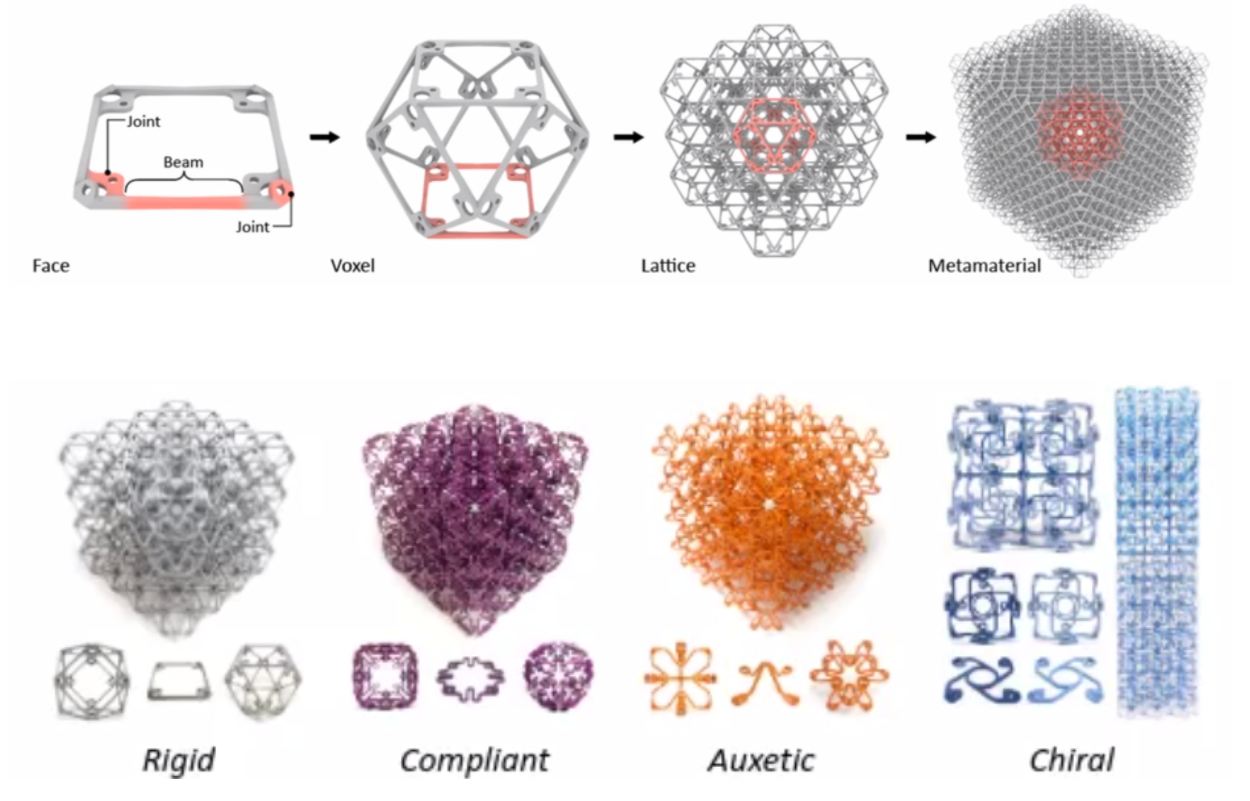
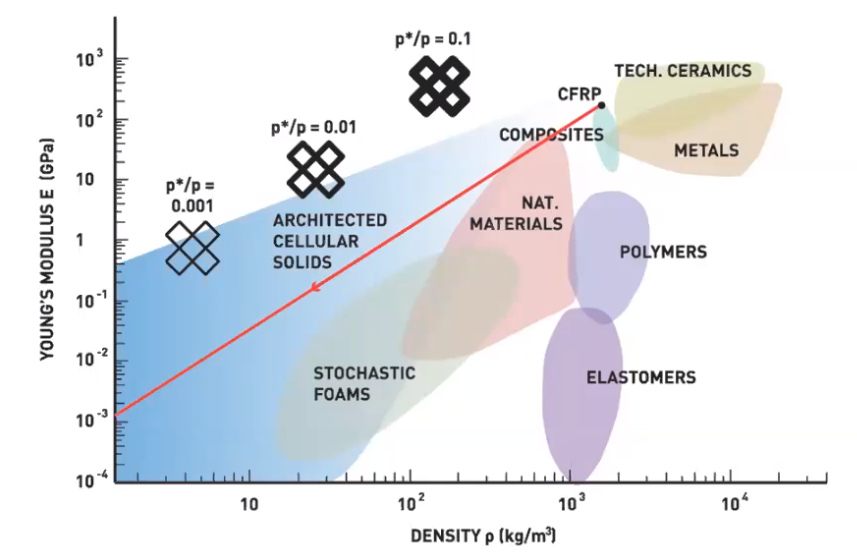
* Benjamin Jenett, Christopher Cameron, Filippos Tourlomousis, Alfonso Parra Rubio,Megan Ochalek, and Neil Gershenfeld. Discretely assembled mechanical metamaterials.Science Advances, 6(47):eabc9943, 2020.
Applications


Test Case Study: Morphing Wing



Project Overview
Inverse Design Process
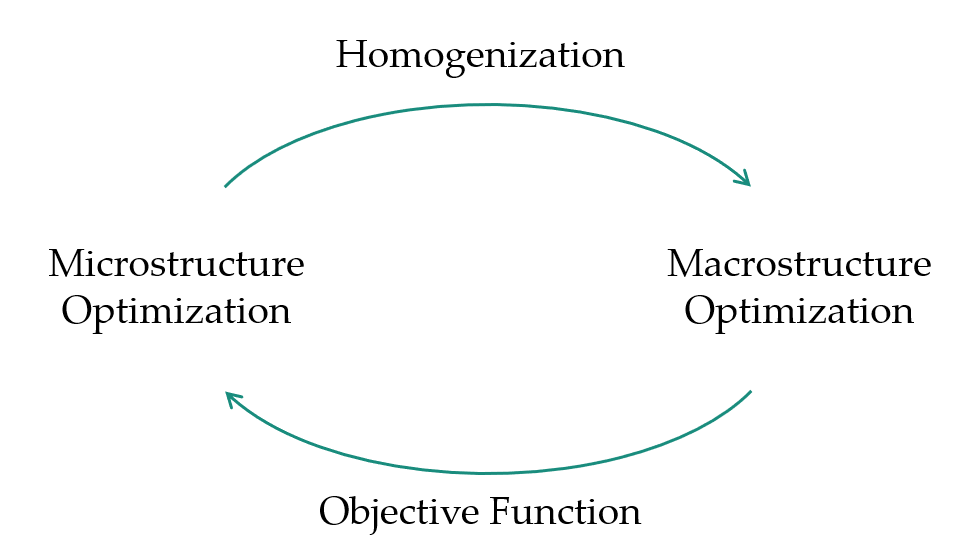
Microstructure Optimization
Compliant Mechanism Design of Trusses
\[ \begin{aligned} & \underset{\rho^e}{\text{minimize}} & & V(\rho^e)=\sum_{e \in \Omega } \rho^e \upsilon^e \\ & \text{subject to} & & K (\rho^e)d-F=0 \\ & & & g= L_i^T d\leq d_{max,i} \ \forall i \in 1,..,m \\ & & & \rho^e_{min} \leq \rho^e \ \forall e \\ & \end{aligned} \]
Using the adjoint method
The gradient of objective function: \[ f= \sum_{e \in \Omega } \rho^e \upsilon^e \\ \frac{\delta f}{\delta \rho_e}=\sum_{e \in \Omega } \upsilon^e \] The gradient of each constraint $i \ \forall (1,..,m)$: \[ \frac{\delta g_A}{\delta \rho_e}= - \lambda_i^T \frac{\delta K(\rho_e)}{\delta \rho_e } d \\ \]
2D Initial Results
3D Initial Compliant Mechanisms Results




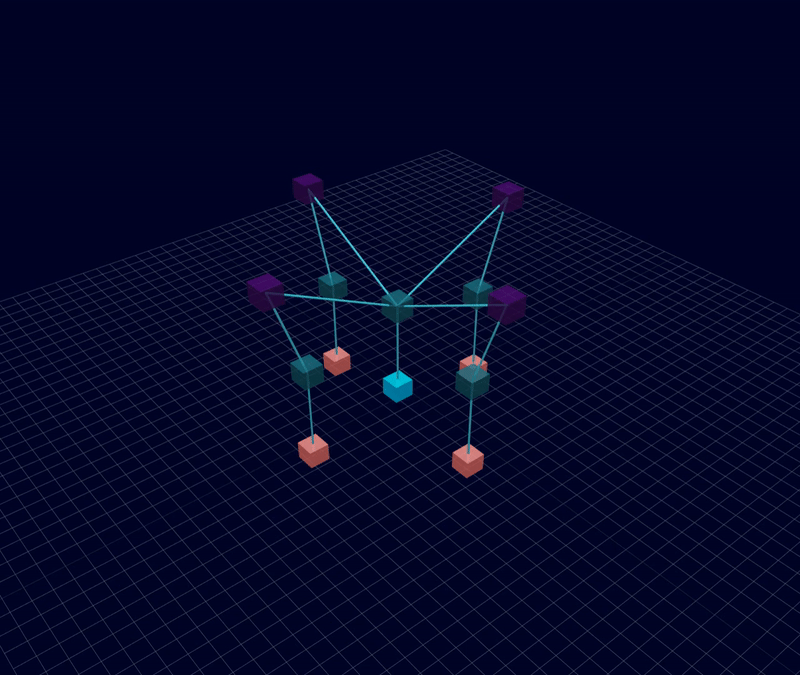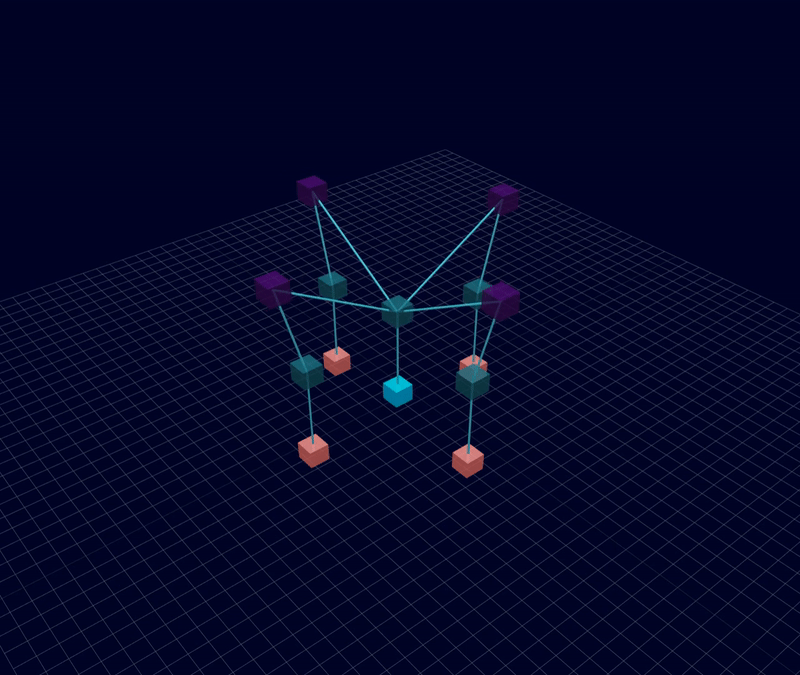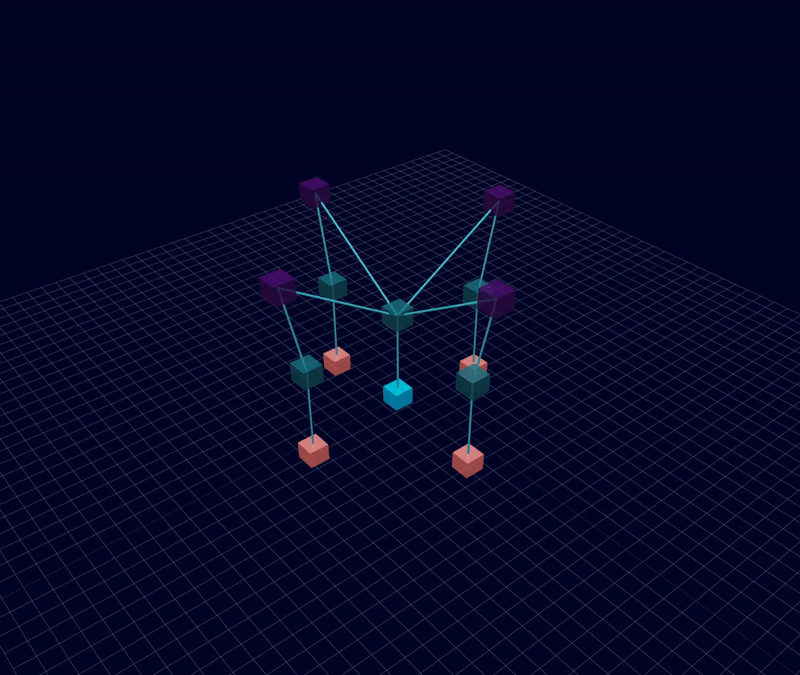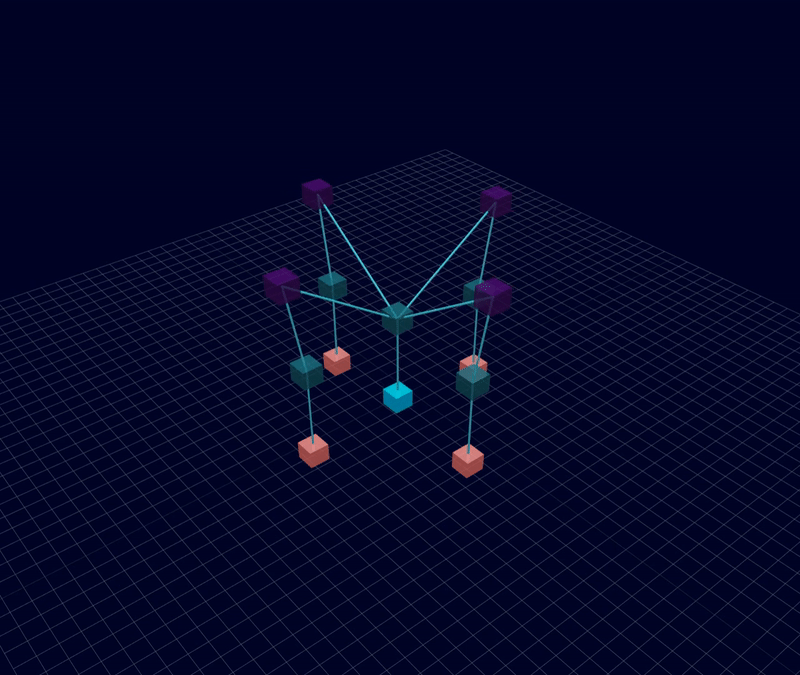
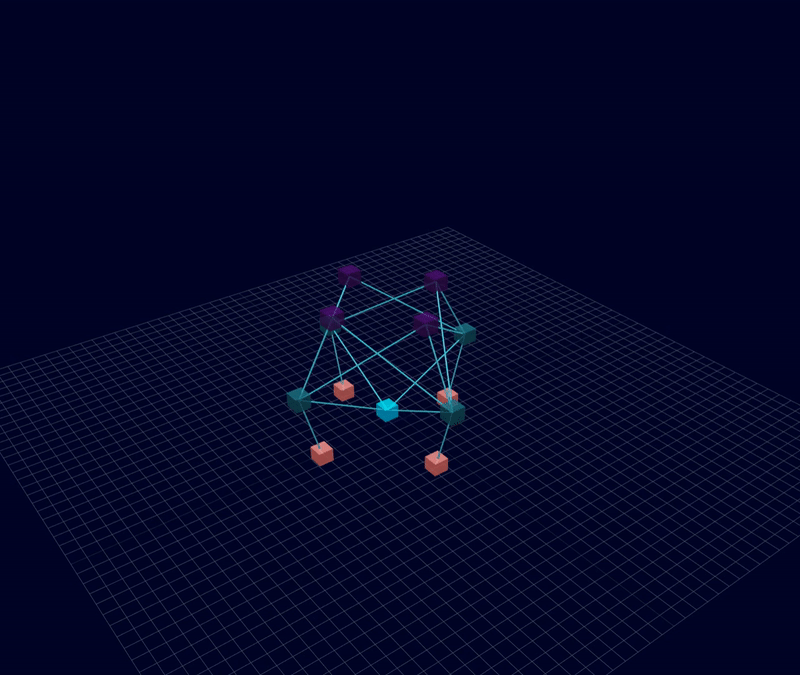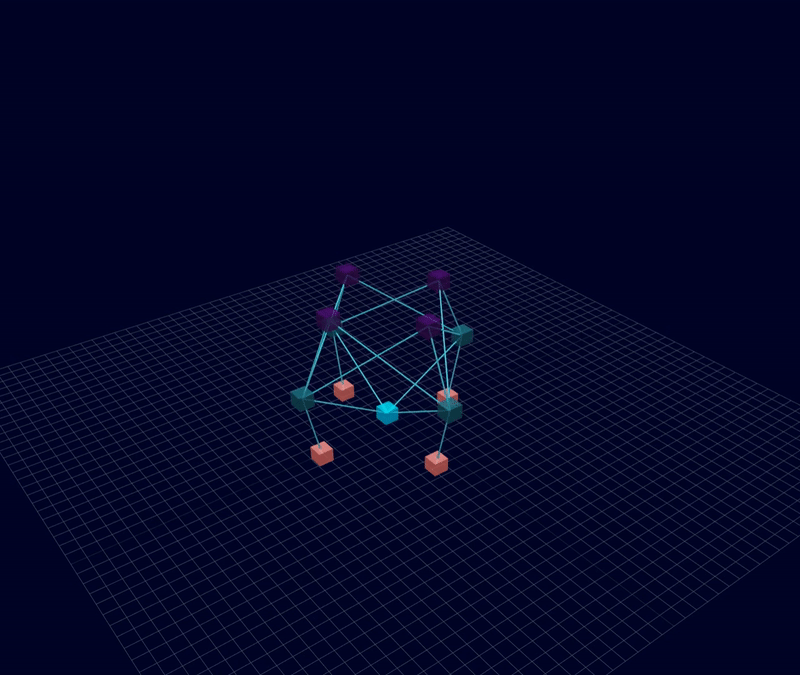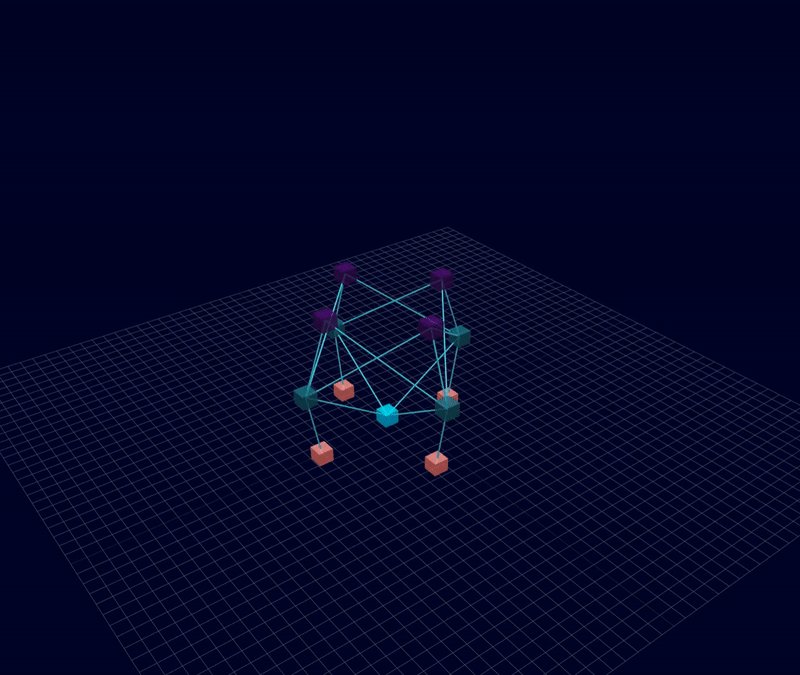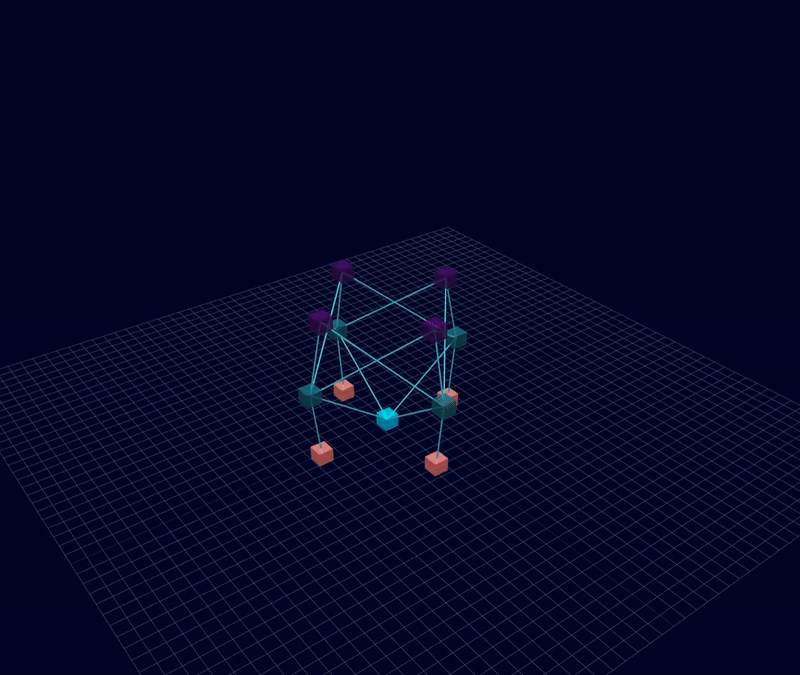
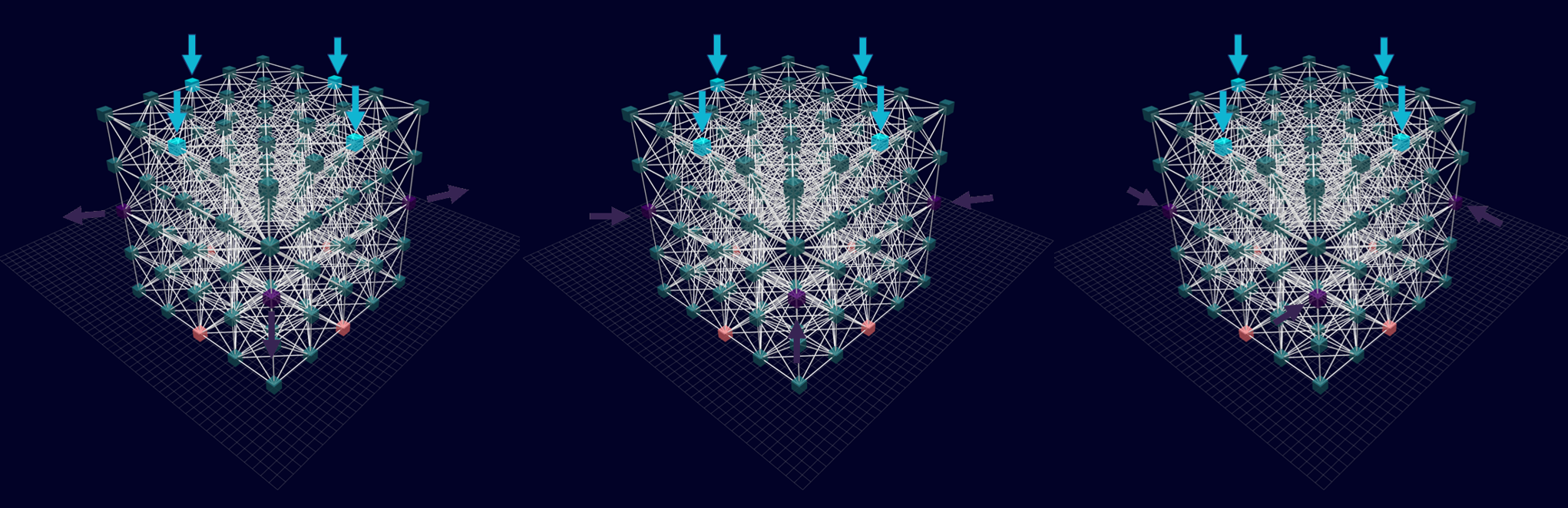
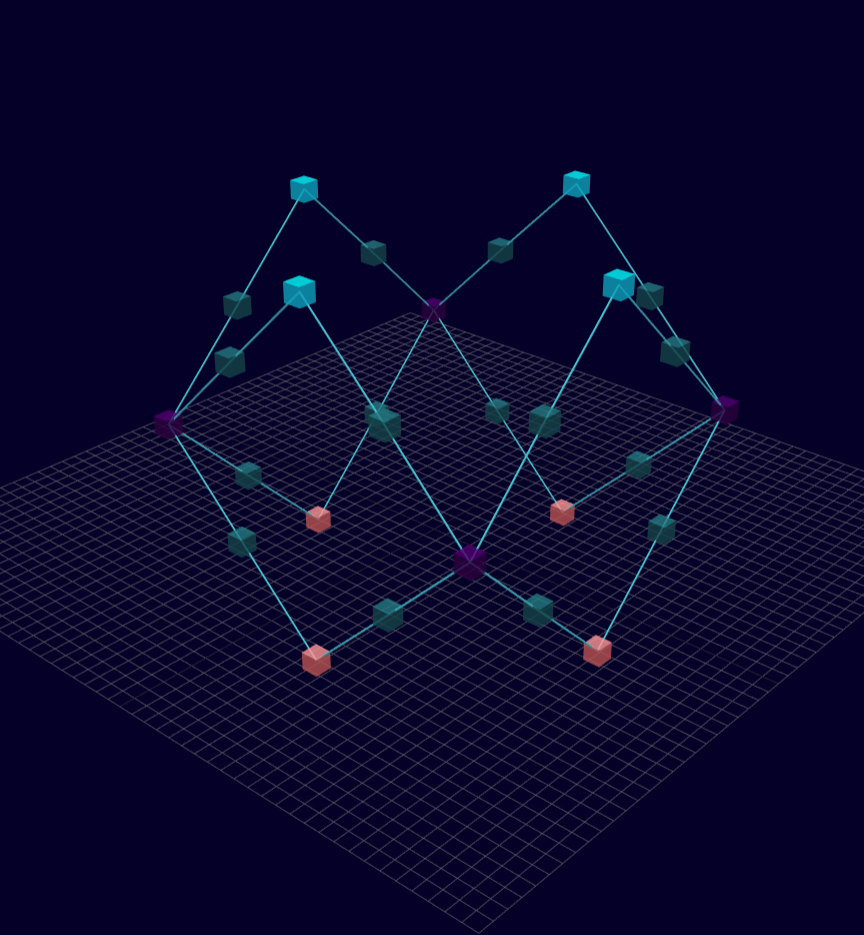
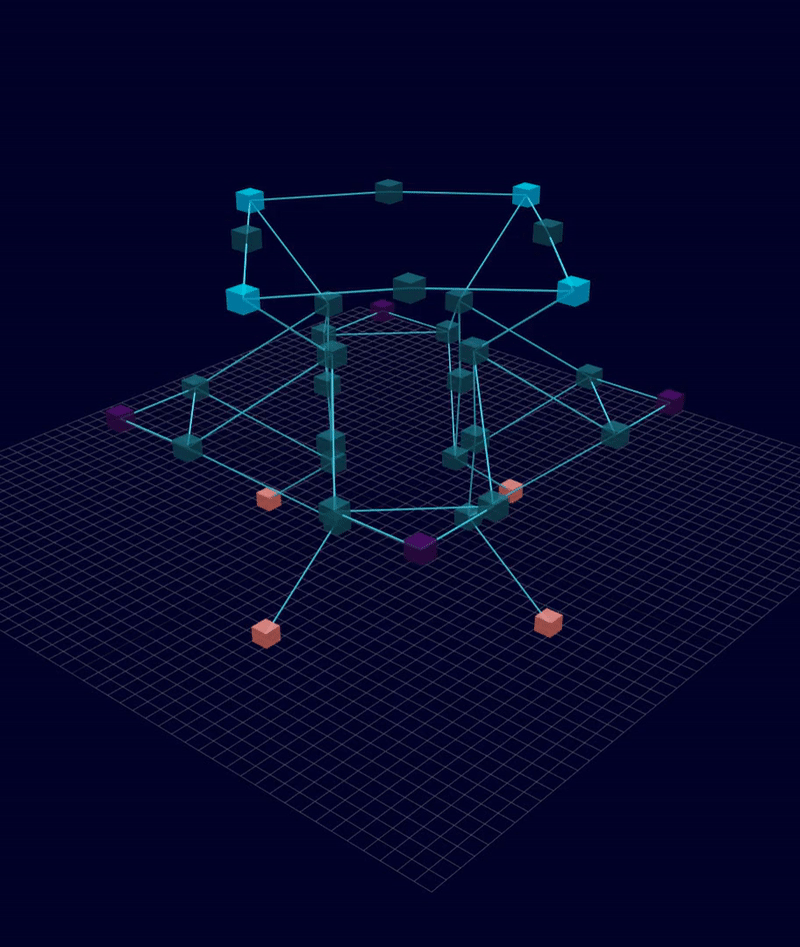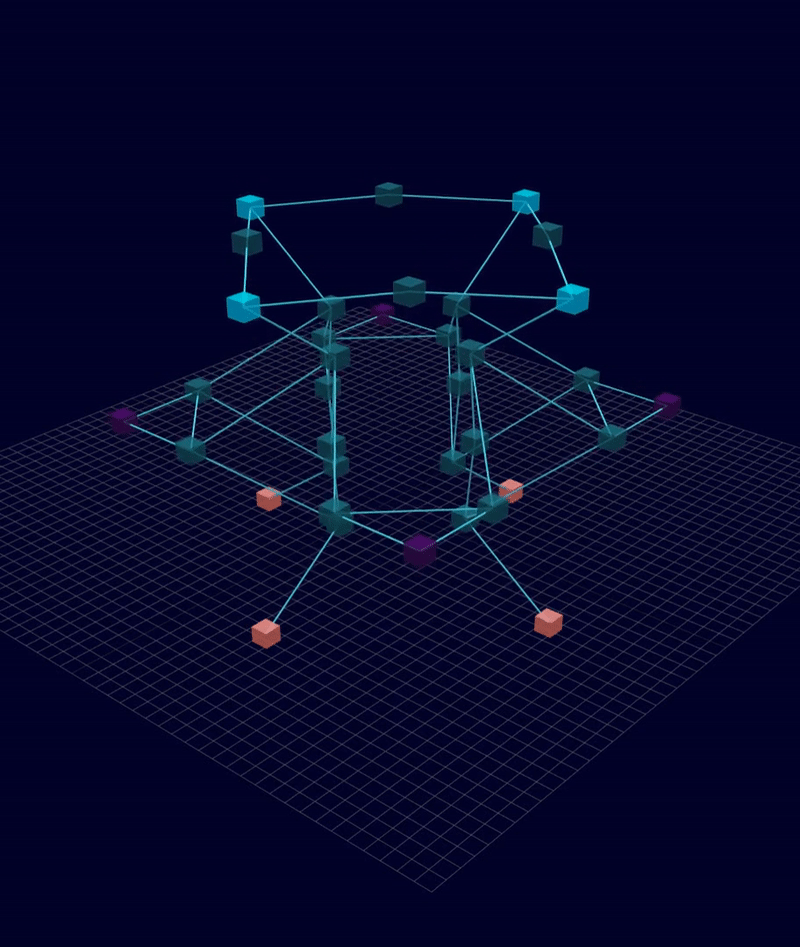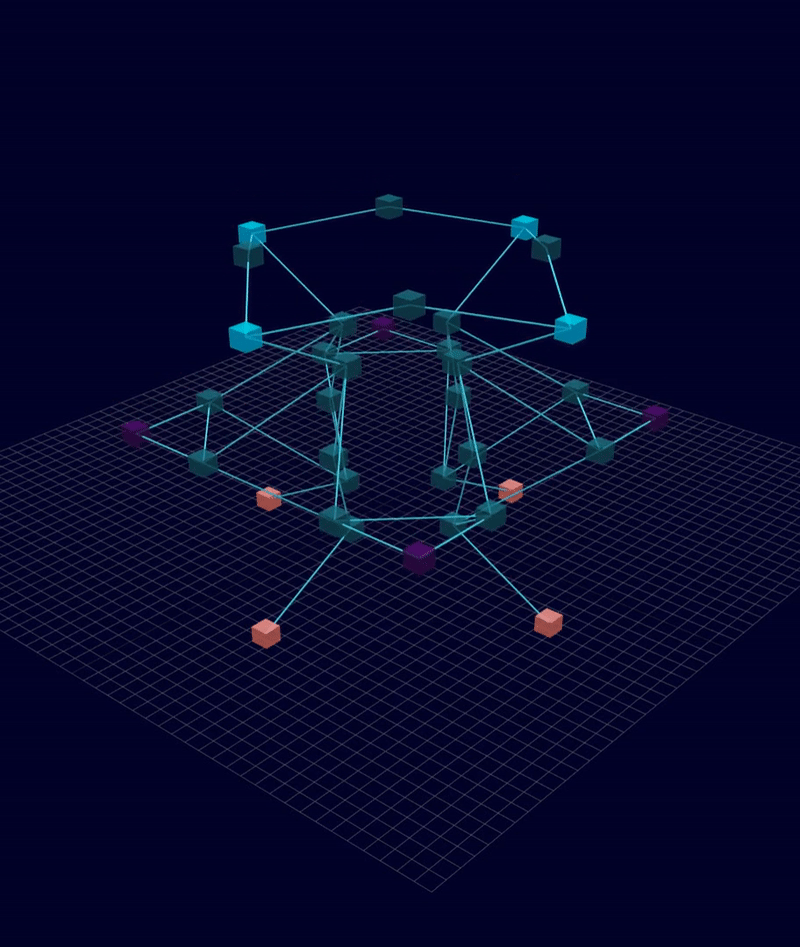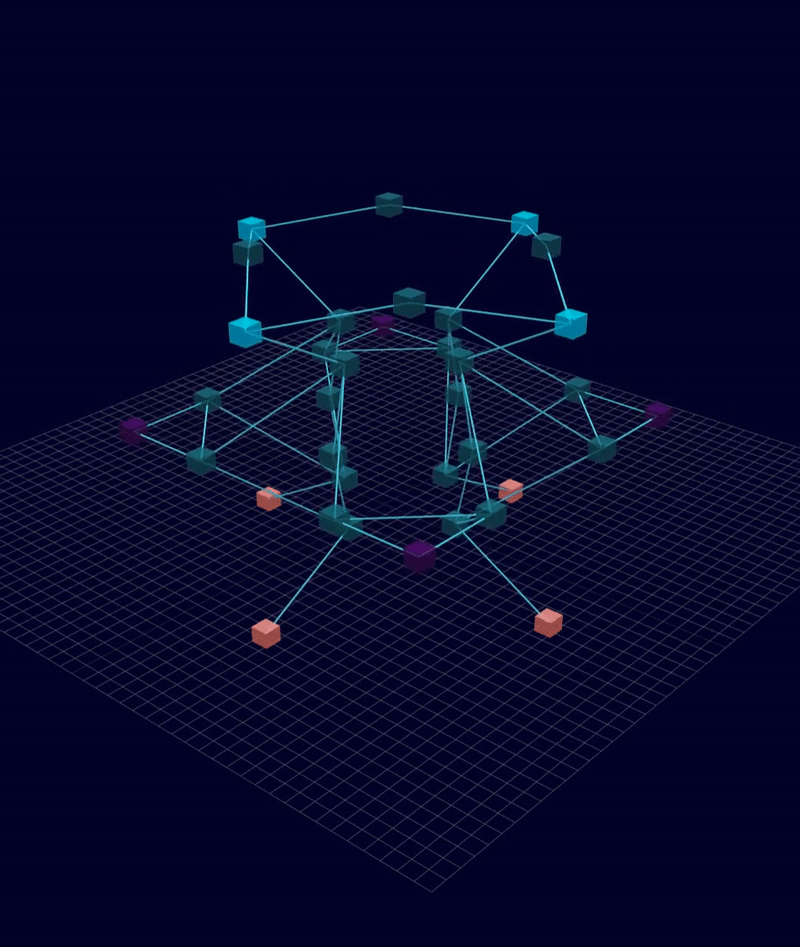
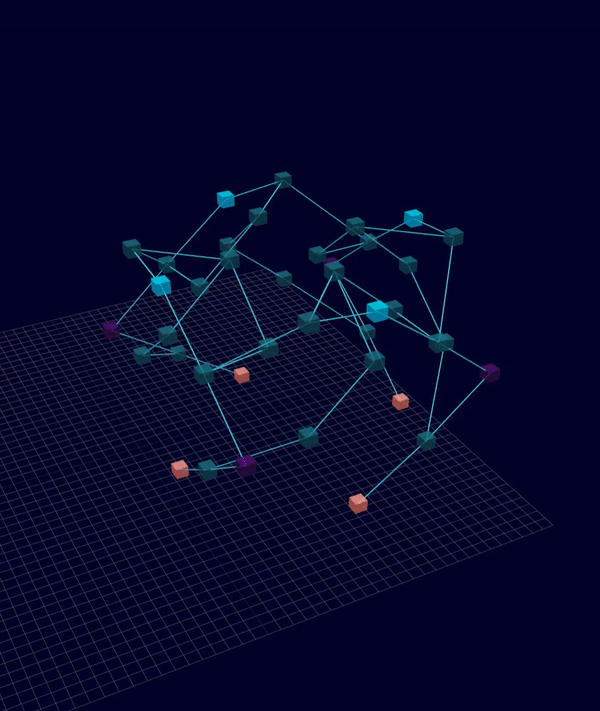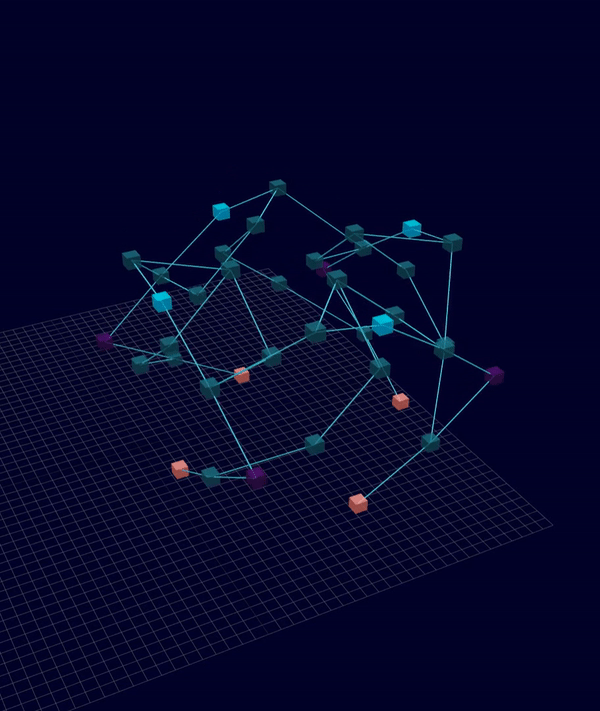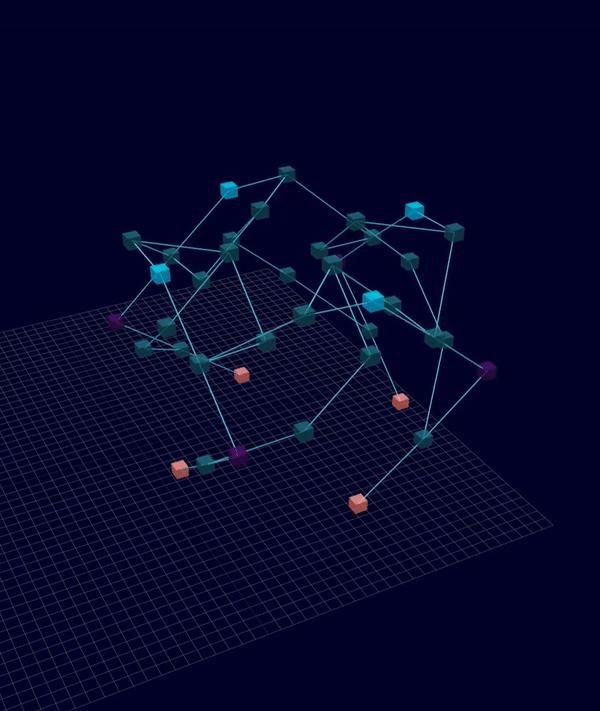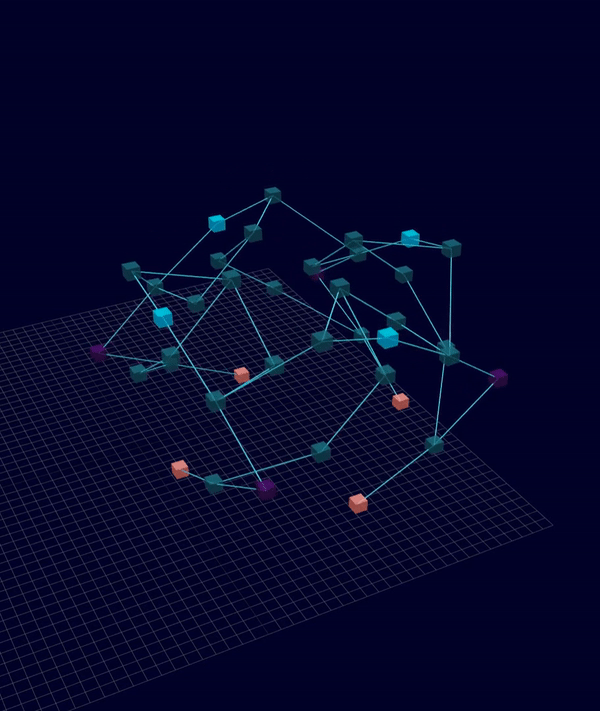
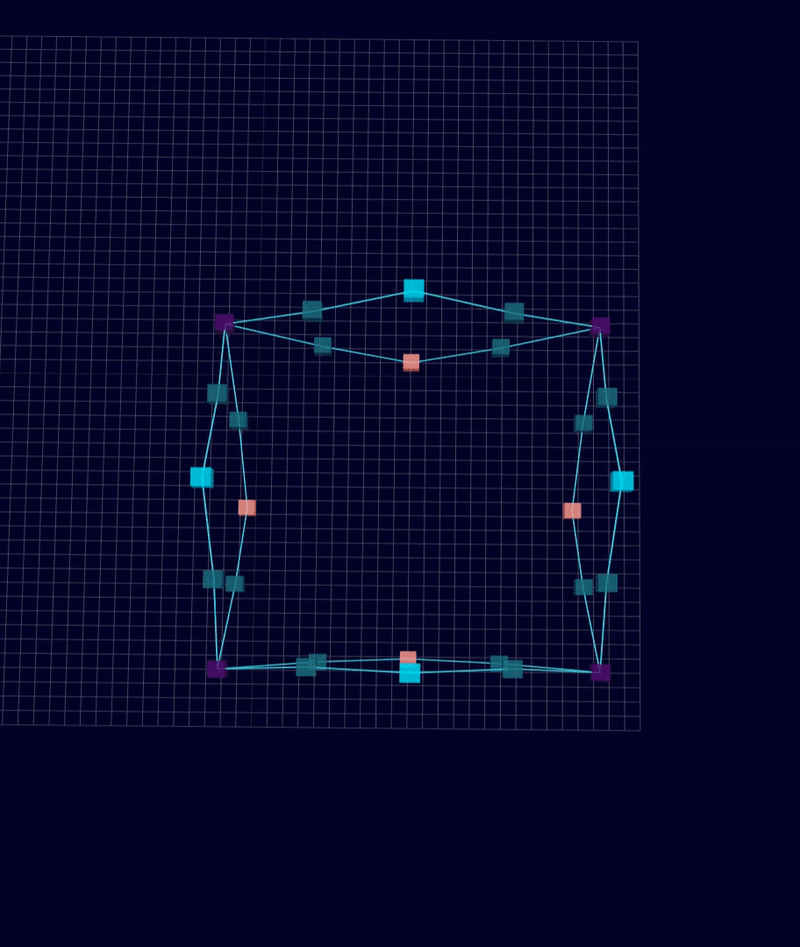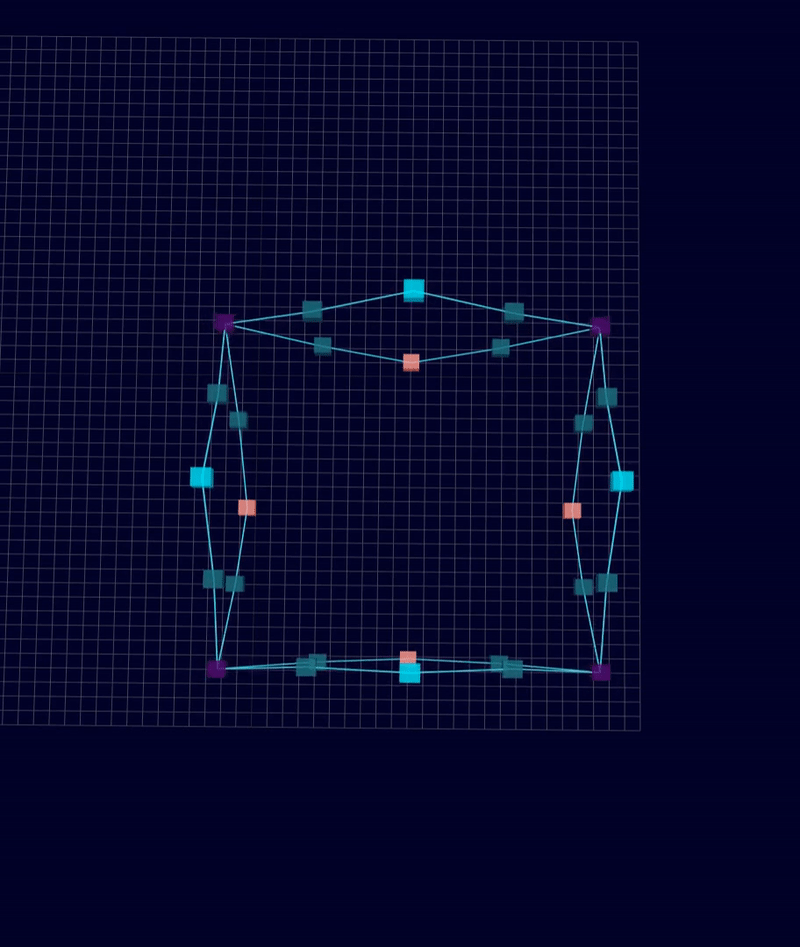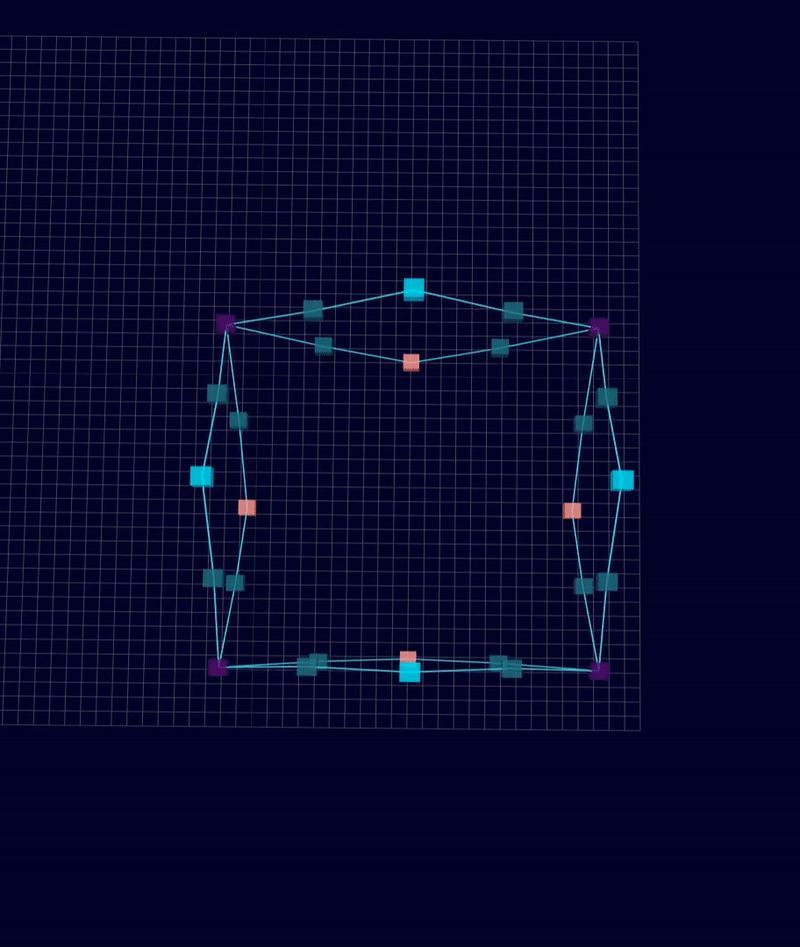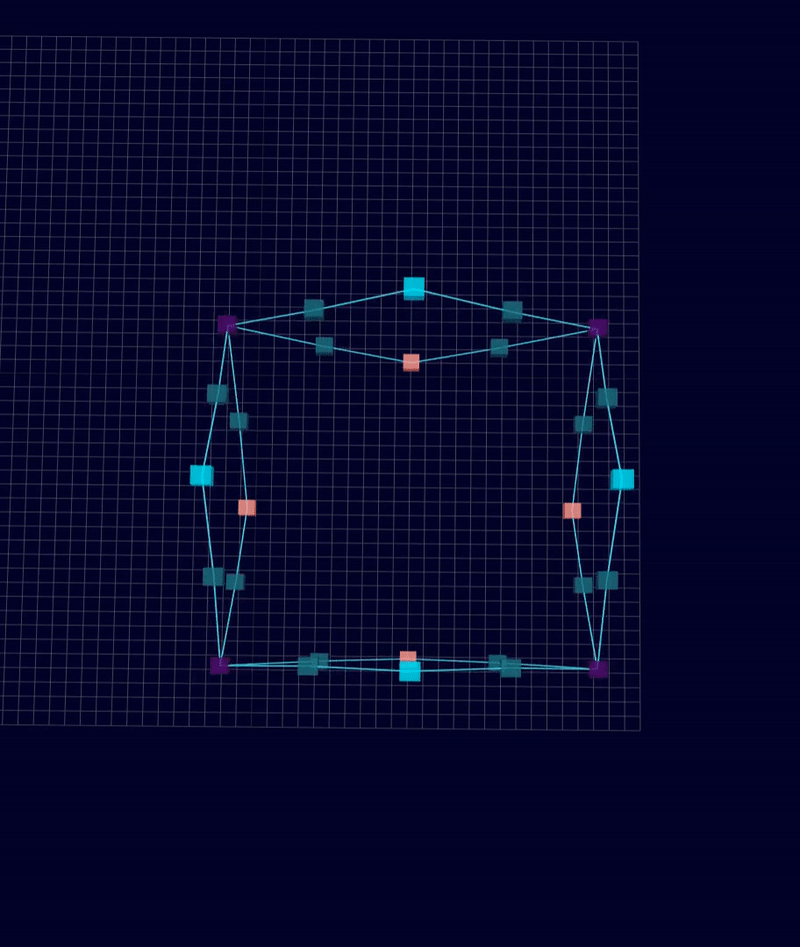
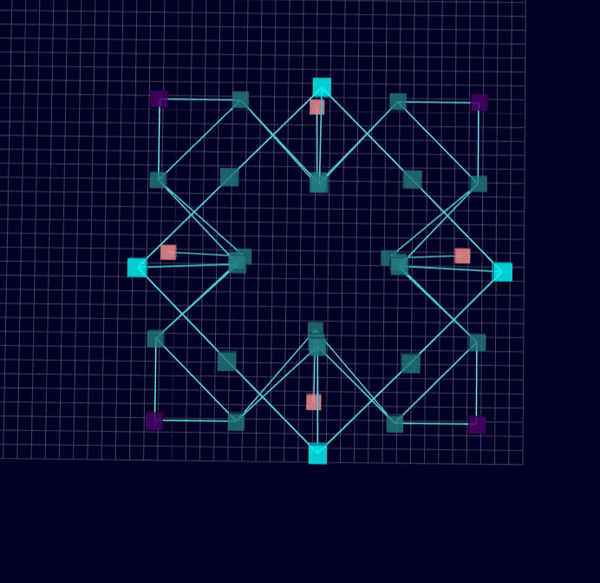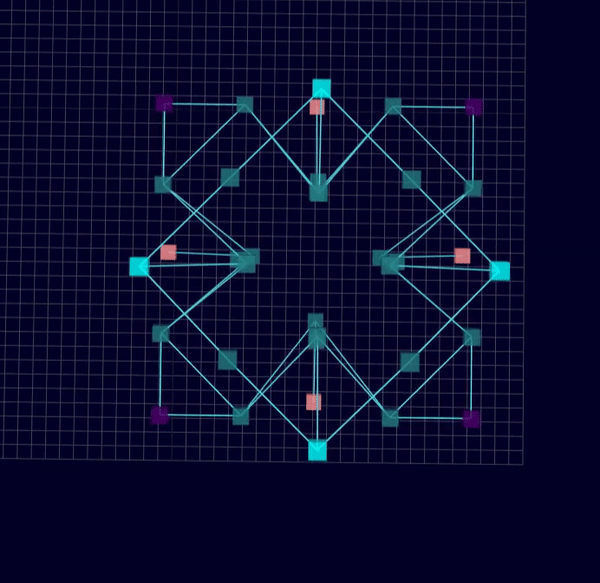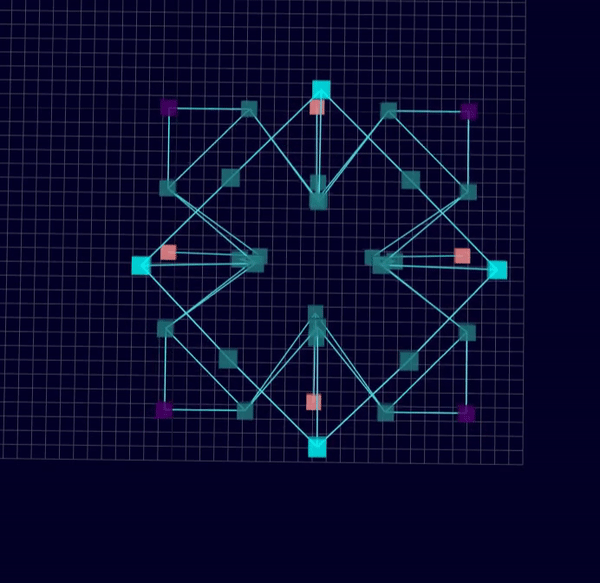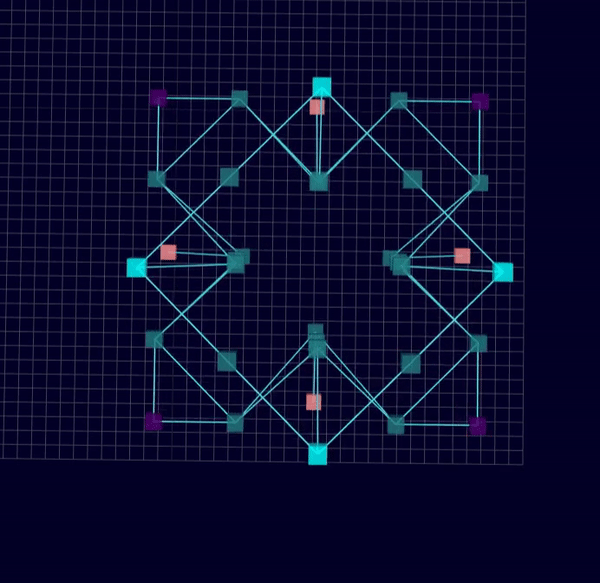
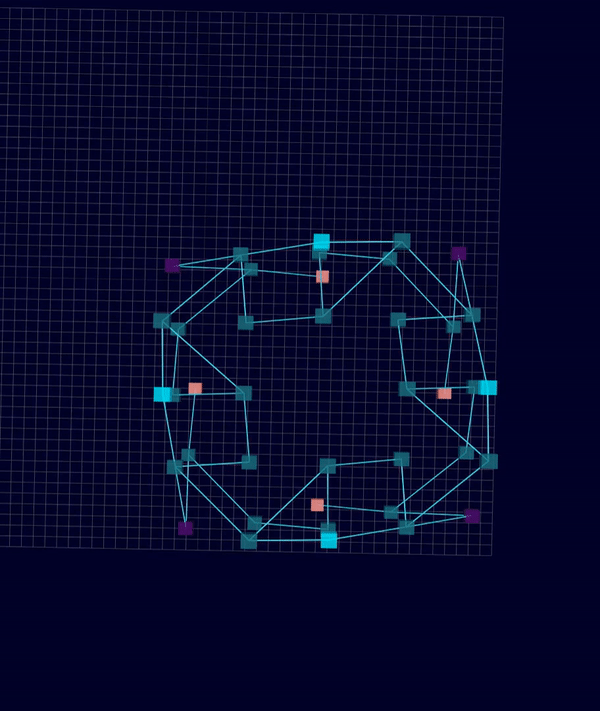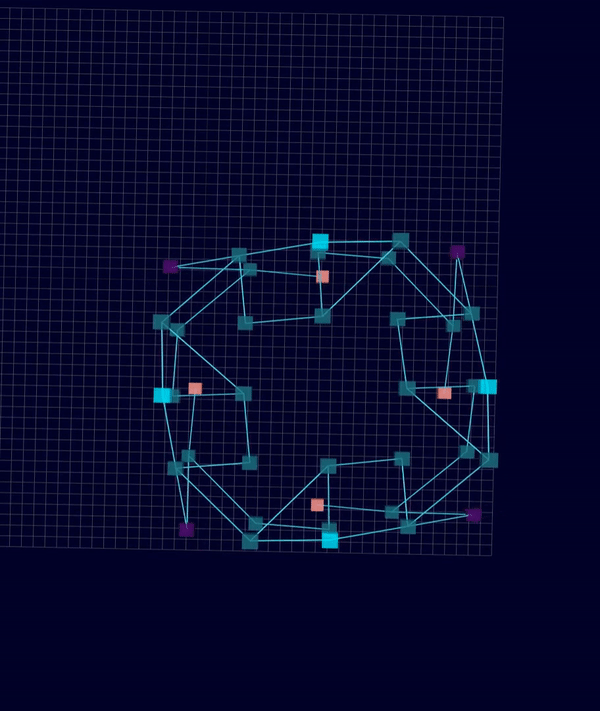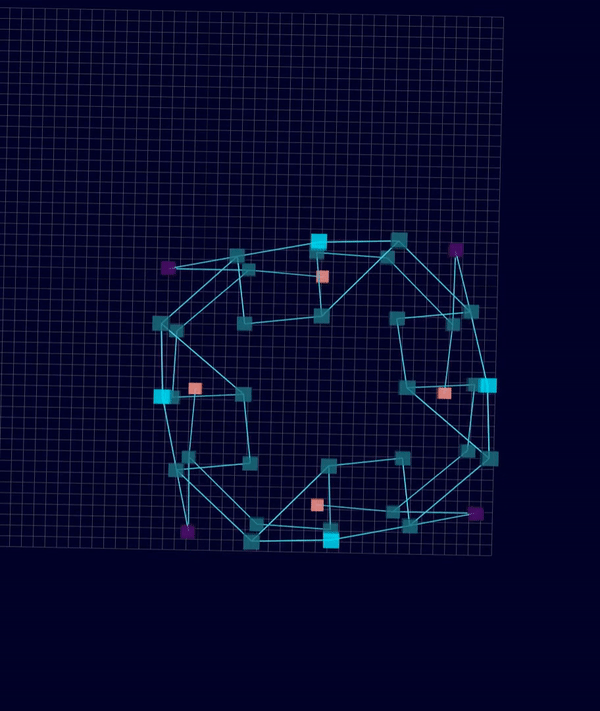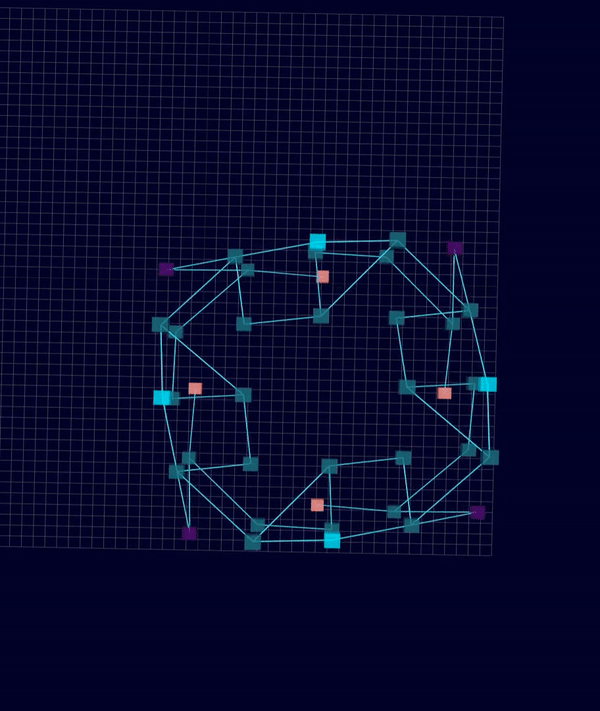
Results: Microstructures after Manual Cleanup
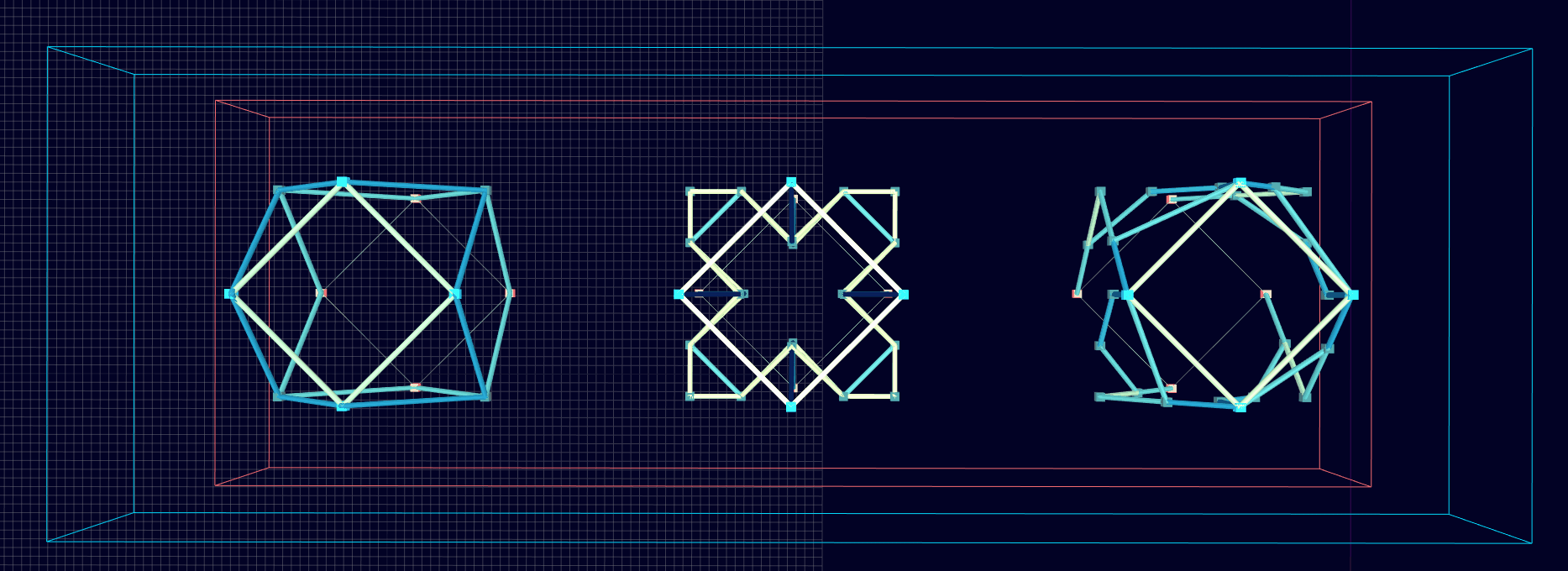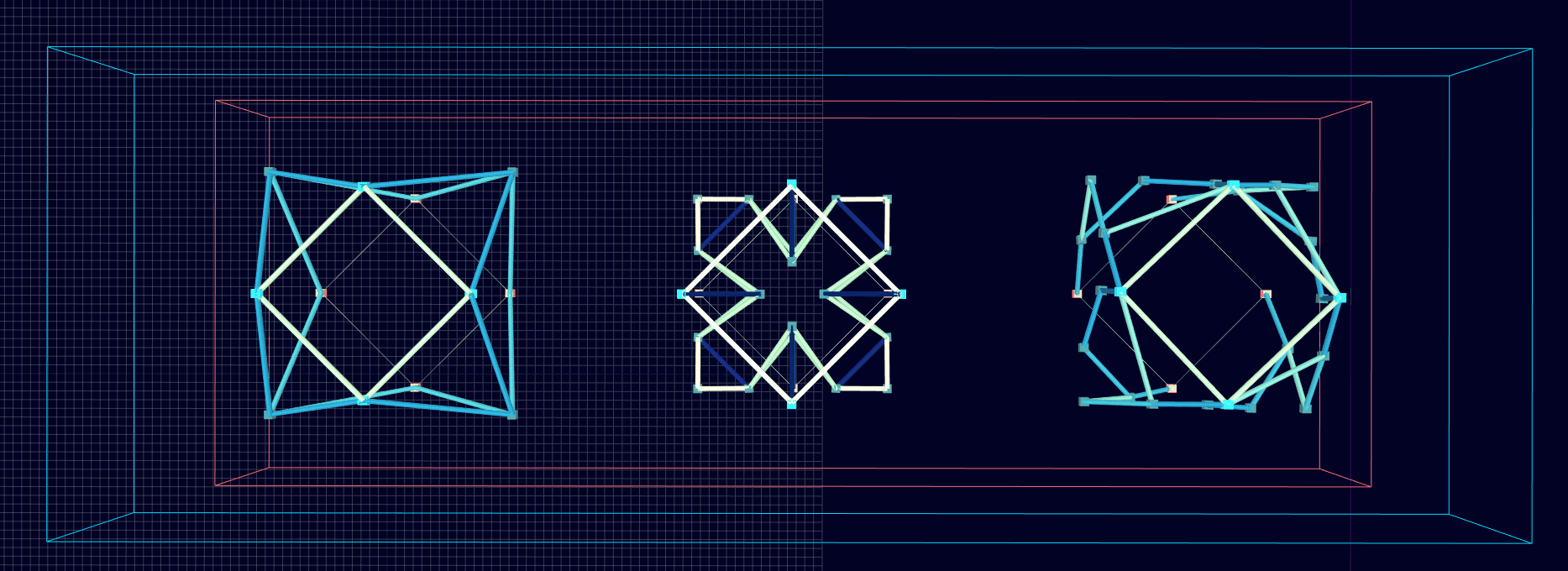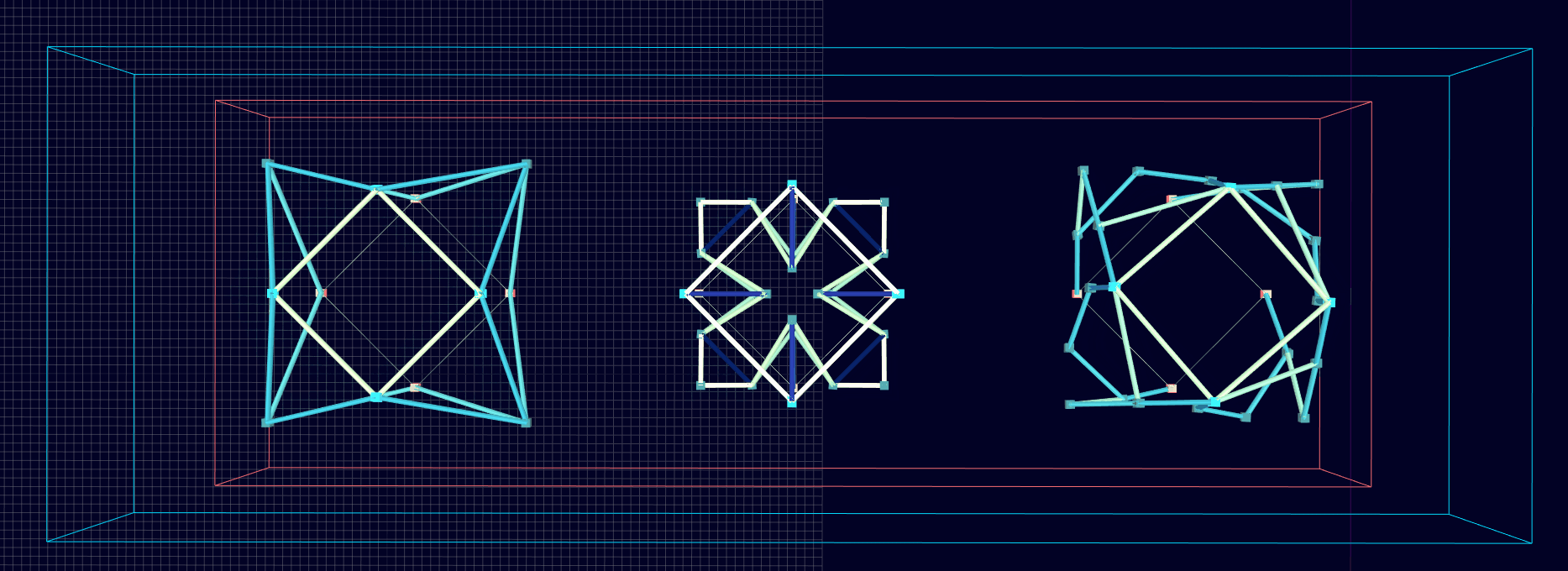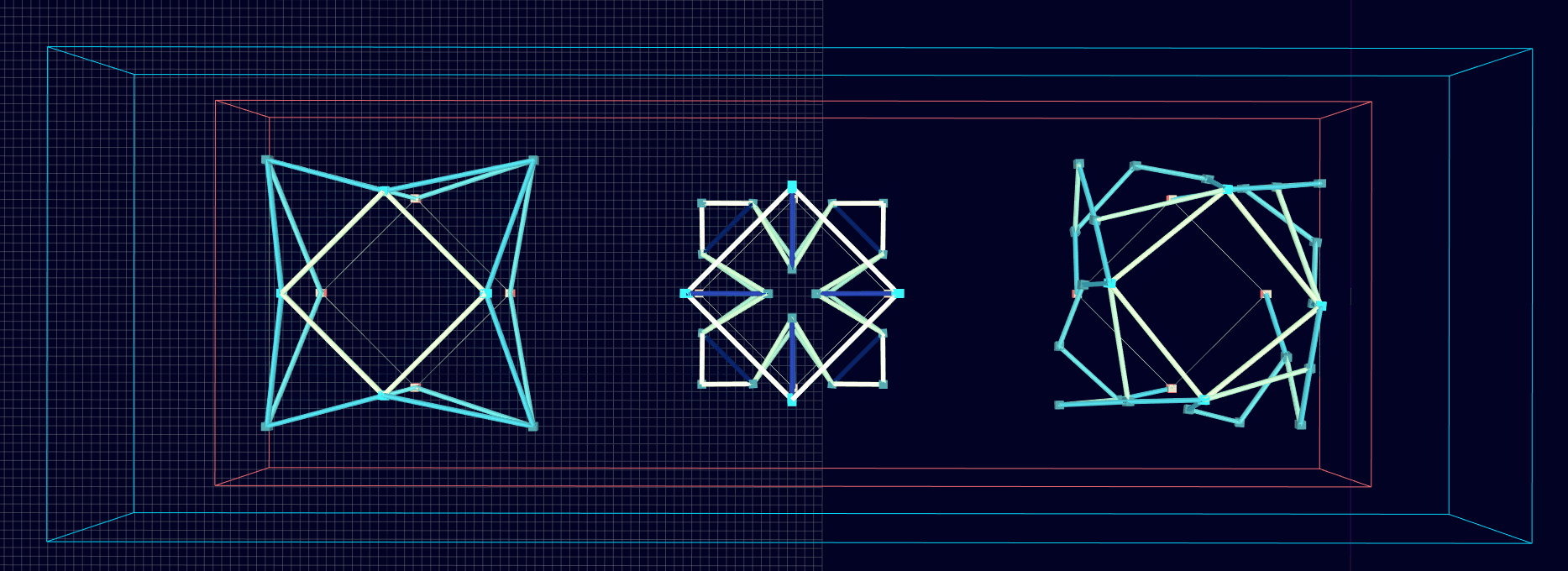
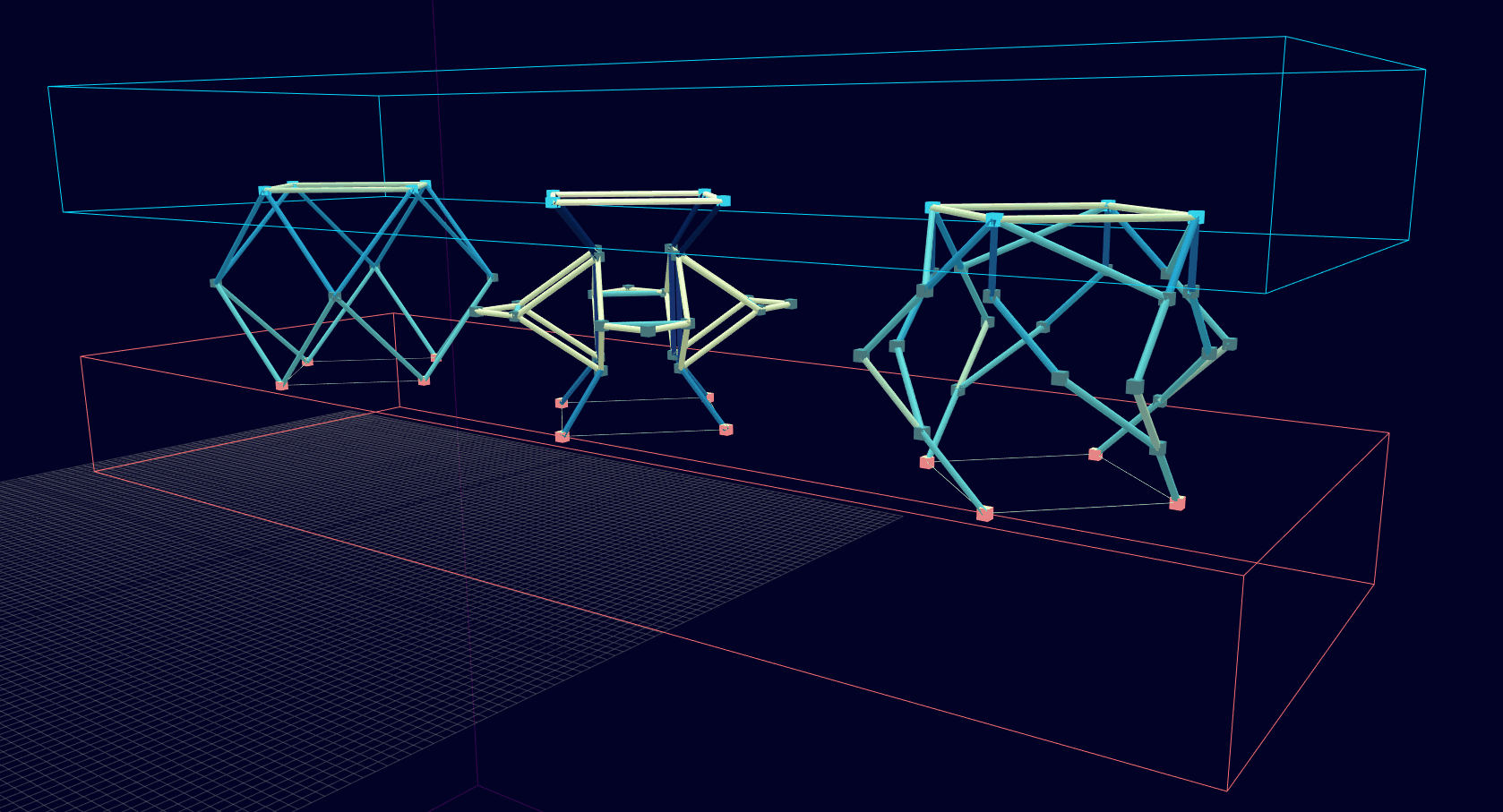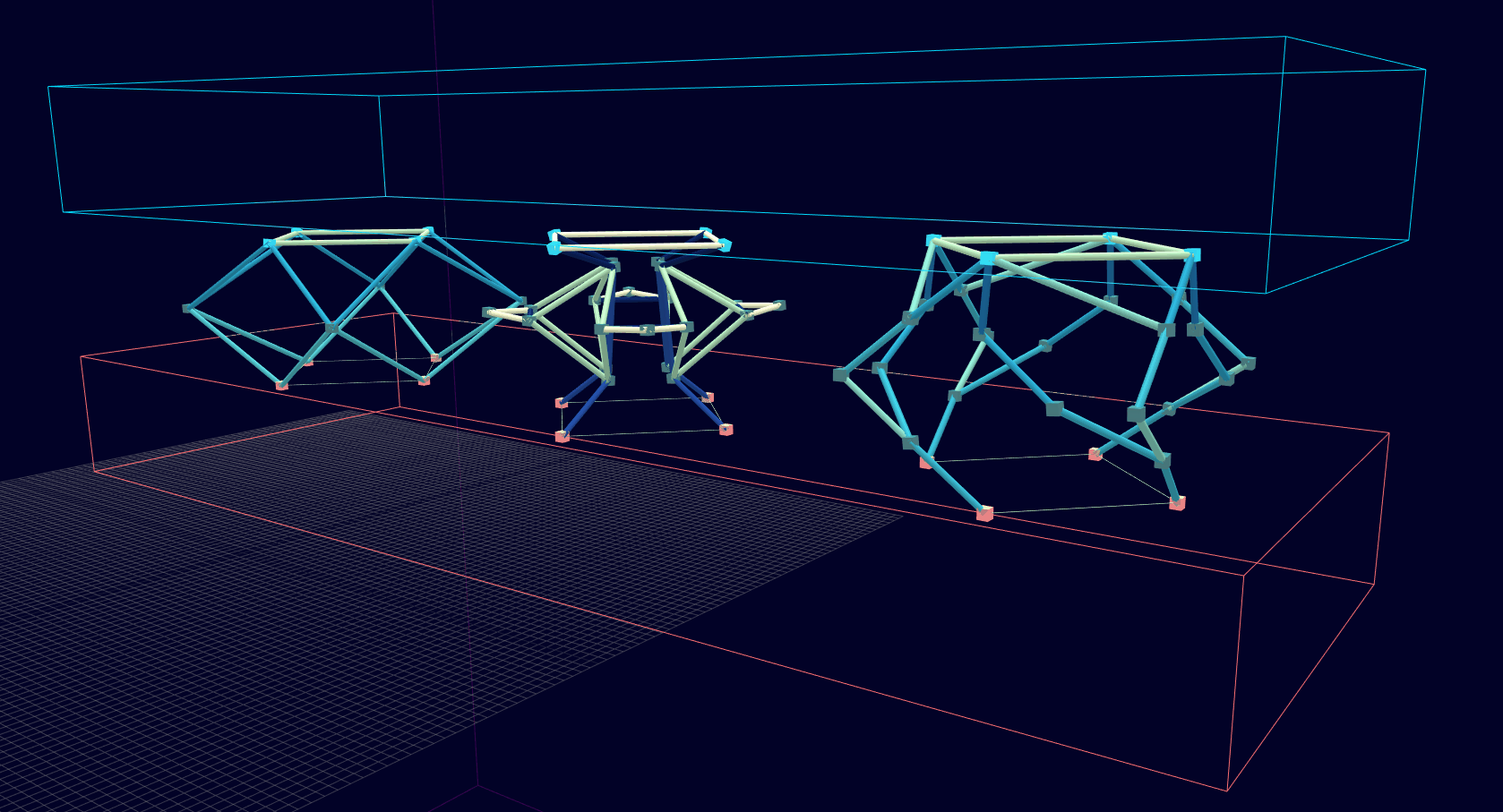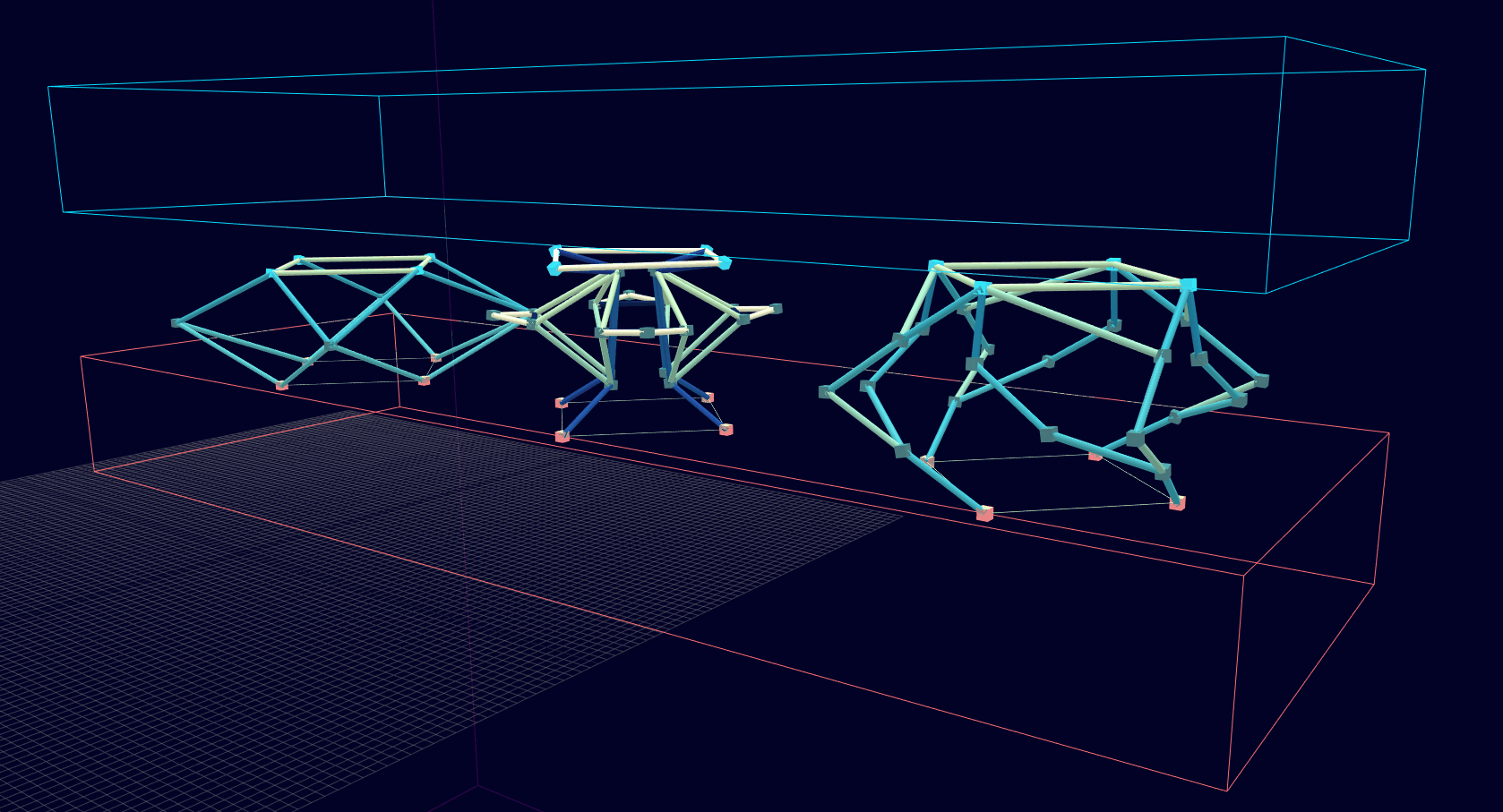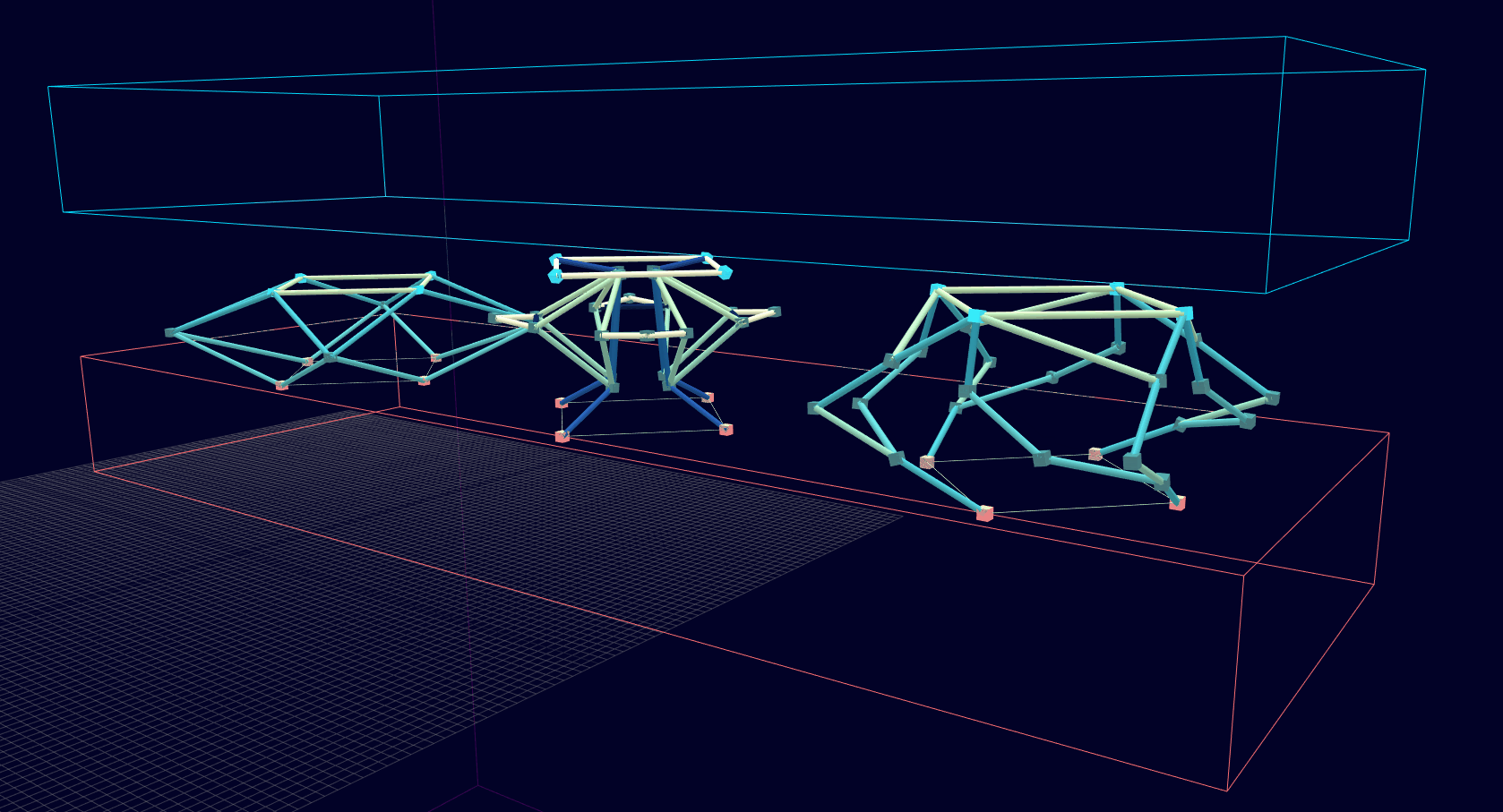
Homogenization
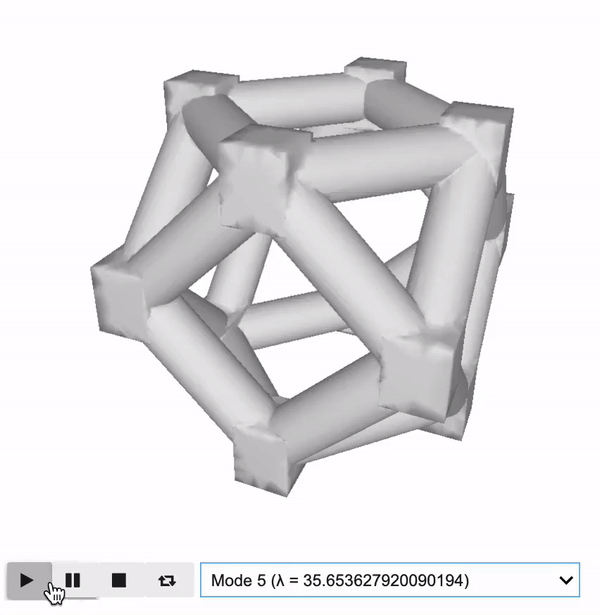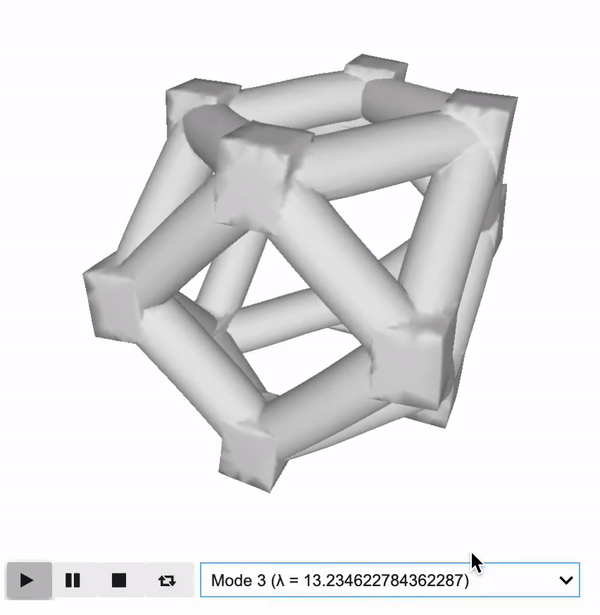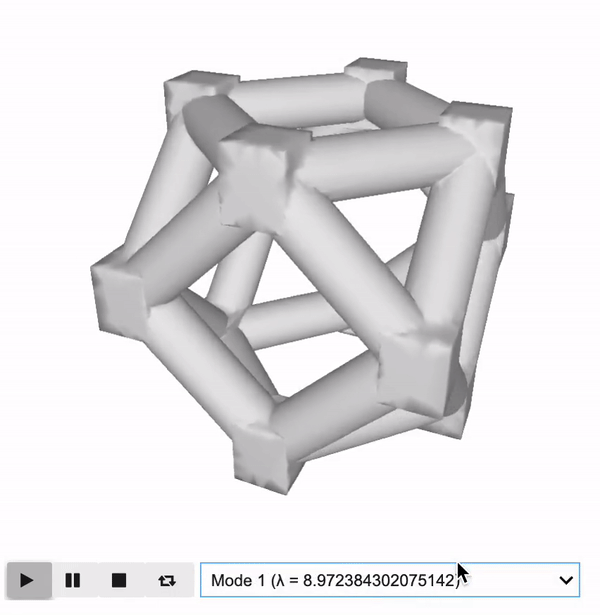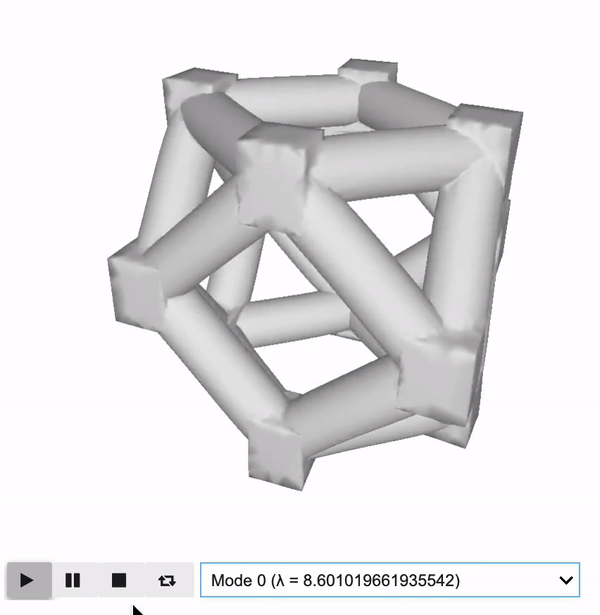
\[ {\mathbf{C}}^H=\frac{1}{\left|{\Omega}_m\right|}{\int}_{\Omega_m}\mathbf{C}\left(\varepsilon \left({\mathbf{u}}_m^0\right)-\varepsilon \left({\mathbf{u}}_m\right)\right)\left(\varepsilon \left({\mathbf{u}}_{\mathrm{m}}^0\right)-\varepsilon \left({\mathbf{u}}_m\right)\right)\mathrm{d}{\Omega}_m \] \[ {\int}_{\Omega_m}\mathbf{C}\varepsilon \left({\mathbf{u}}_{\boldsymbol{m}}\right)\varepsilon \left({\boldsymbol{\nu}}_m\right)\mathrm{d}{\Omega}_m={\int}_{\Omega_m}\mathbf{C}\varepsilon \left({\mathbf{u}}_m^0\right)\varepsilon \left({\boldsymbol{\nu}}_m\right)\mathrm{d}{\Omega}_m,\kern1.25em \forall {\boldsymbol{\nu}}_m\mathbf{\in}{H}_{per}\left({\Omega}_m,{\mathbb{R}}^d\right) \]
Homogenization Results
Youngs Modulus
| Lattice | E11 | E22 | E33 |
|---|---|---|---|
| Cube | 6.9e7 | 6.9e7 | 6.9e7 |
| Cuboct | 9.85e7 | 9.85e7 | 9.85e7 |
| Auxetic | 2.584e8 | 1.608e8 | 1.608e8 |
| Chiral | 1.12e8 | 1.14e8 | 1.14e8 |
Shear Modulus
| Lattice | G23 | G31 | G12 |
|---|---|---|---|
| Cube | 1.45e6 | 1.45e6 | 1.45e6 |
| Cuboct | 5.04e7 | 5.04e7 | 5.04e7 |
| Auxetic | 3.34e7 | 6.78e7 | 3.34e7 |
| Chiral | 5.45e7 | 6.4e7 | 5.45e7 |
Poisson Ratio
| Lattice | v12 | v13 | v23 | v21 | v31 | v32 |
|---|---|---|---|---|---|---|
| Cube | 0.056 | 0.056 | 0.056 | 0.056 | 0.056 | 0.056 |
| Cuboct | 0.294 | 0.294 | 0.294 | 0.294 | 0.294 | 0.294 |
| Auxetic | 0.063 | 0.063 | 0.376 | 0.039 | 0.039 | 0.376 |
| Chiral | 0.2 | 0.2 | 0.43 | 0.21 | 0.21 | 0.43 |
Macrostructure Optimization
Multi-Material Topology Optimization
The materials distribution is determined by the local volume fraction fields, α i (i = 1, … , p) \[ \boldsymbol{A}^{h} := \left\{ \alpha^{h} \in \left\{\alpha_{i}^{h} \in \boldsymbol{V}^{h}\left(\Omega^{h}\right)\right\}_{i\in \{1, \ldots, p\}} \left| \begin{array}{l} \\\\\\ \end{array} \right.\right. \] \[ \left. \begin{array}{ll} \sum_{i=1_{}}^{p} \alpha_{i}^{h} = 1, & \\ \int_{\Omega^{h}_{}} \alpha_{i}^{h} \ dx = \Lambda_{i} |\Omega^h|,\quad & i=1, \ldots, p \\ \boldsymbol{l}_{i}^{h} \leqslant \alpha_{i}^{h} \leqslant \boldsymbol{u}_{i}^{h}, \quad & i=1, \ldots, p \end{array} \right\} \]Implementation Results: MBB and Gripper
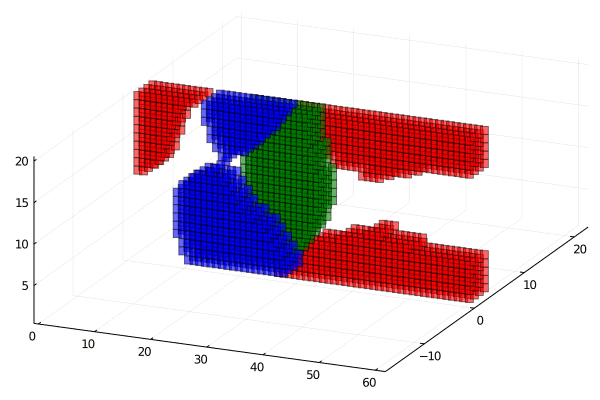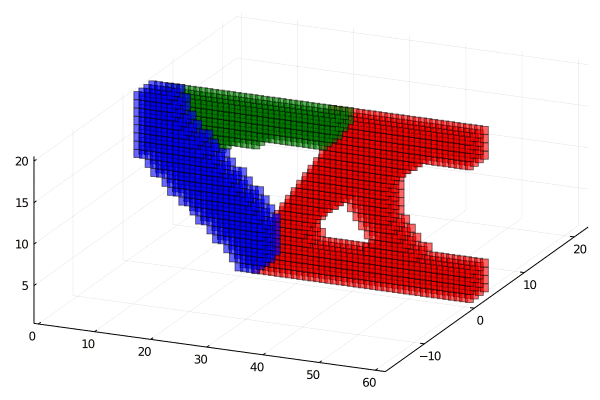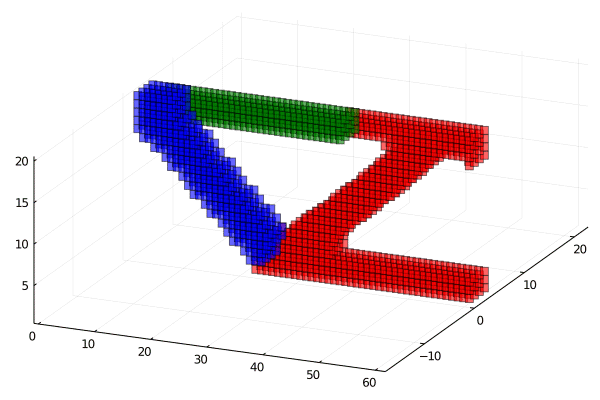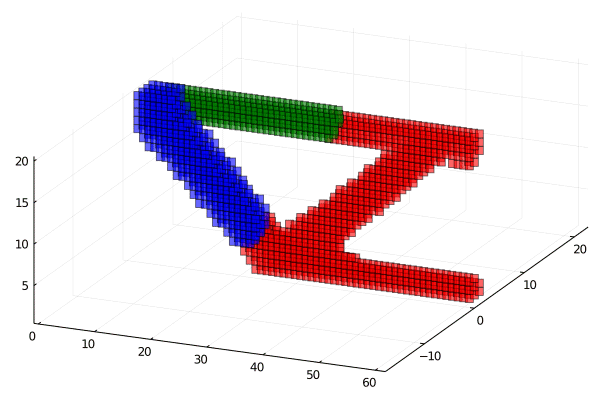
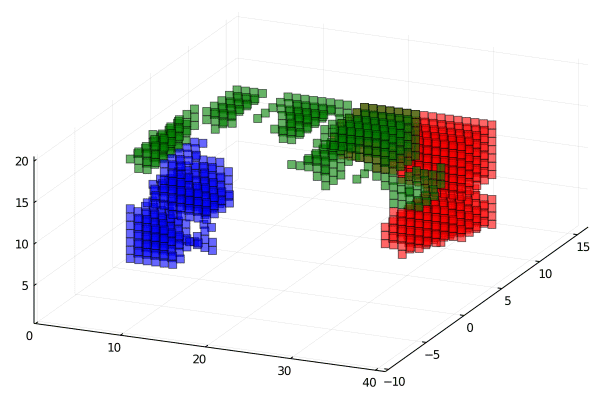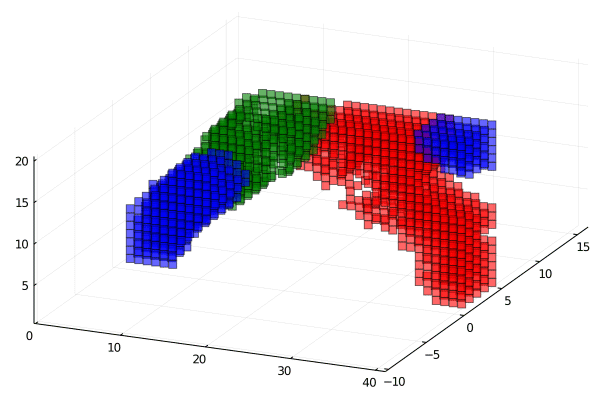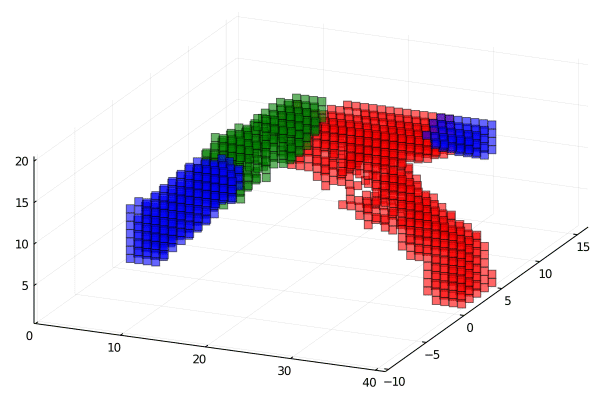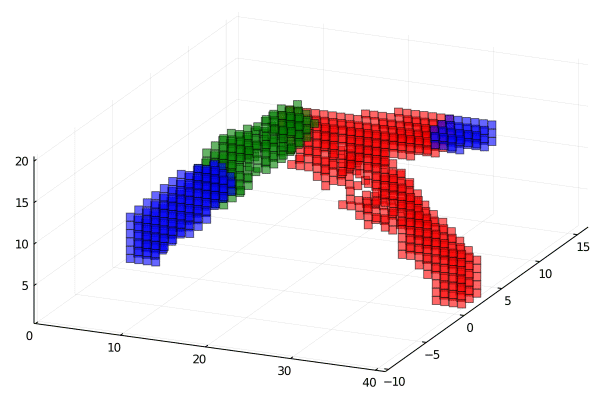
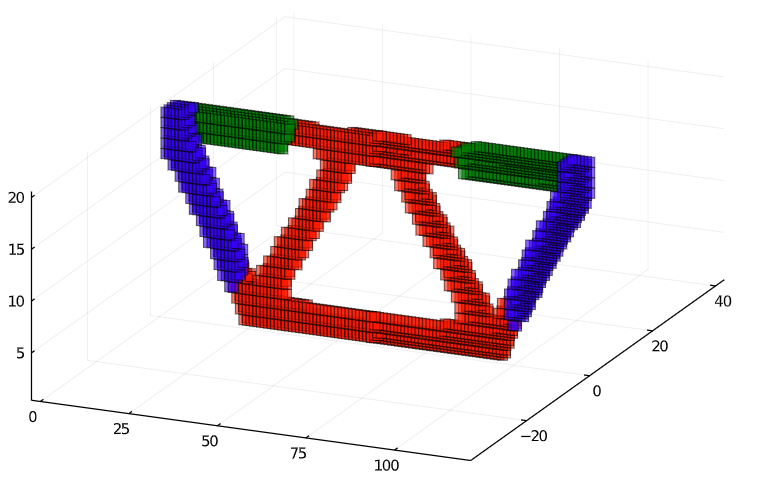
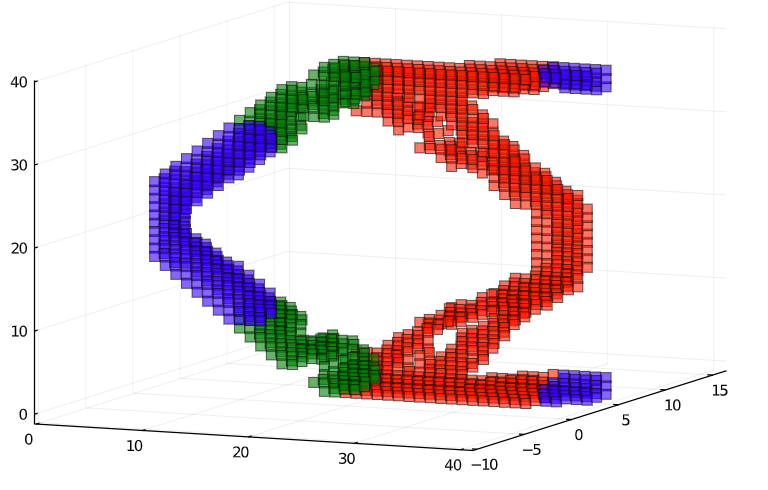
Extended code to 3D and implemented compliance objective
Hierarchal Topology Optimization
Cube Cuboct
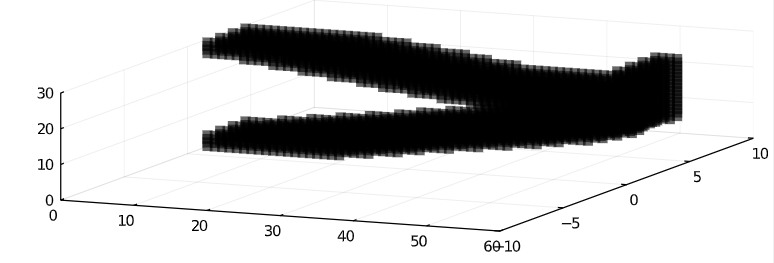
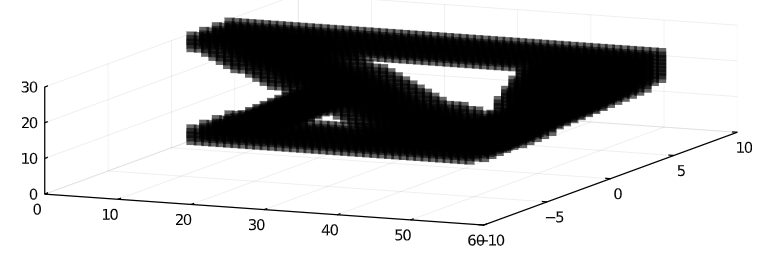
Auxetic Chiral
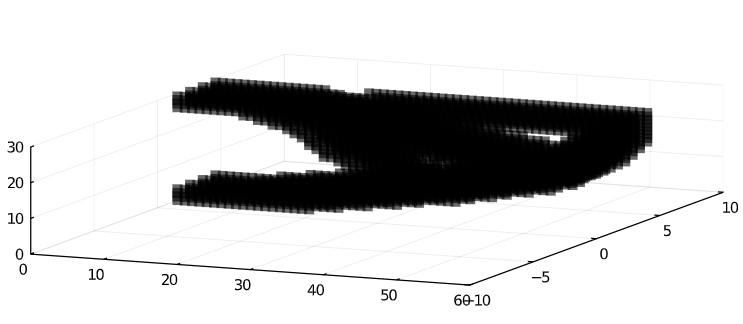
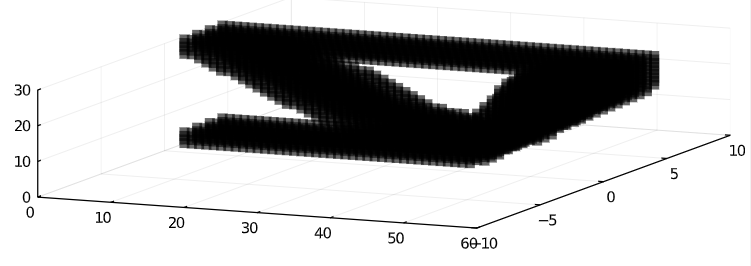
Morphing Wing Problem Formulation
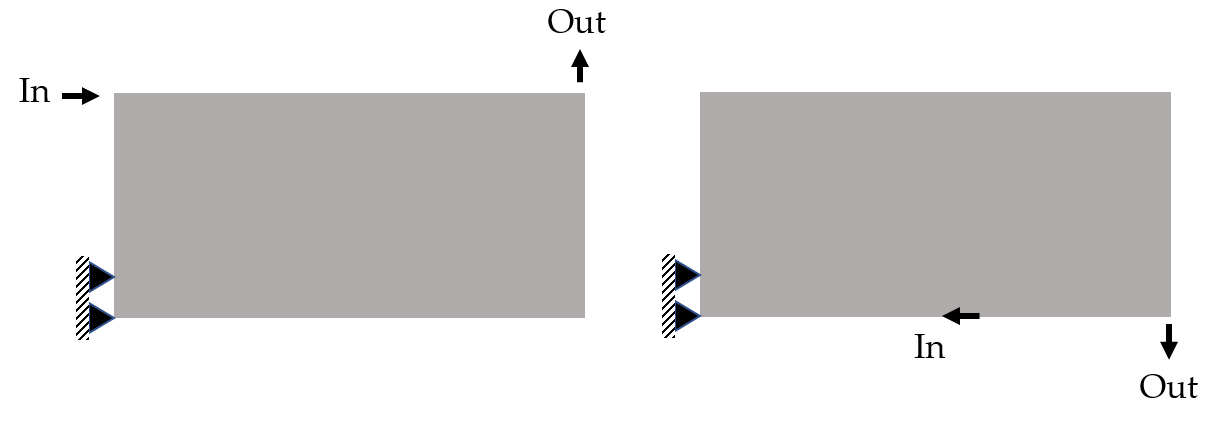
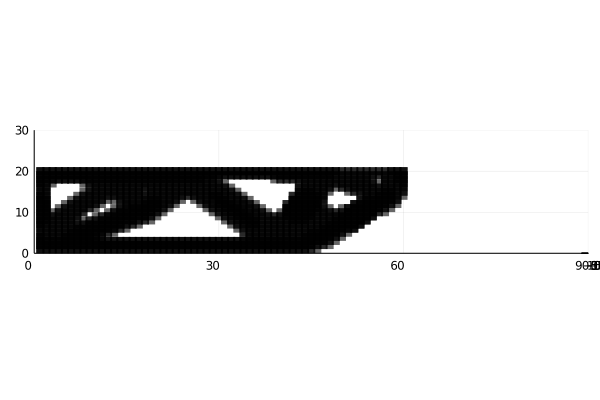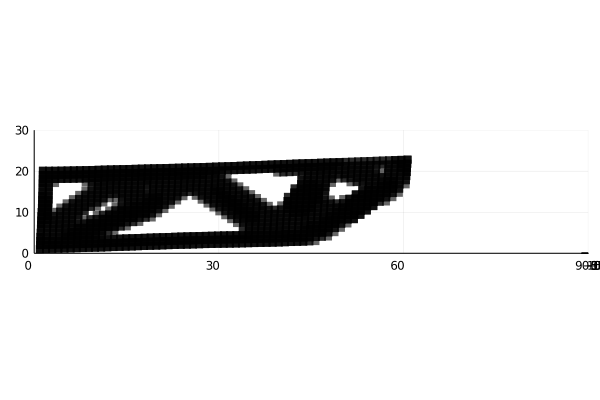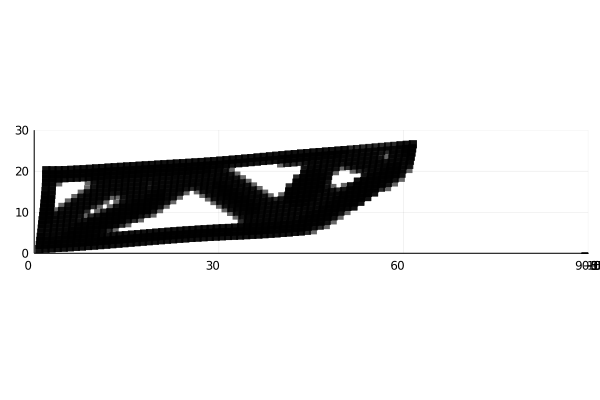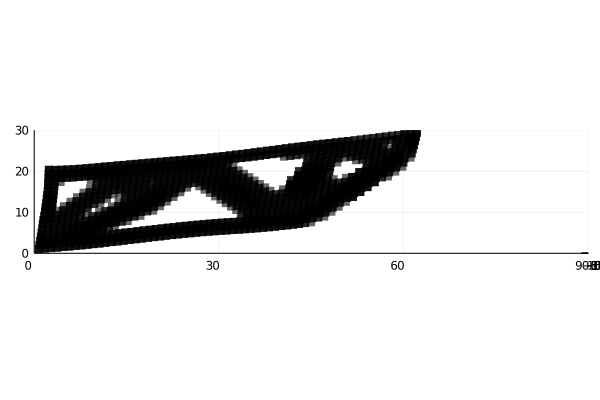
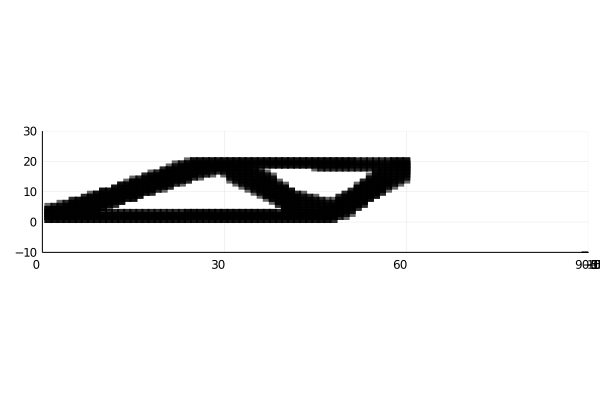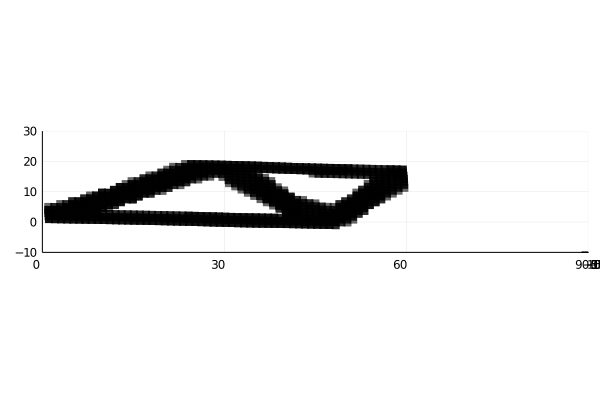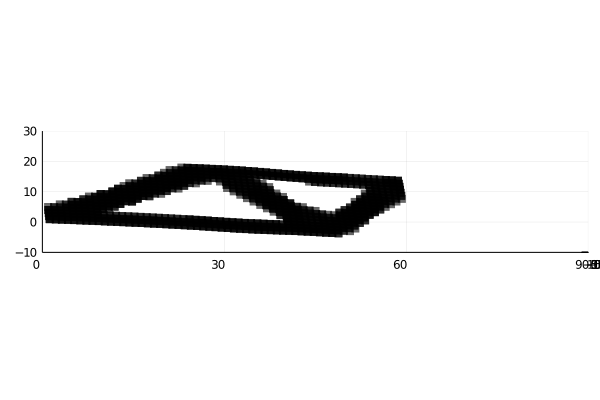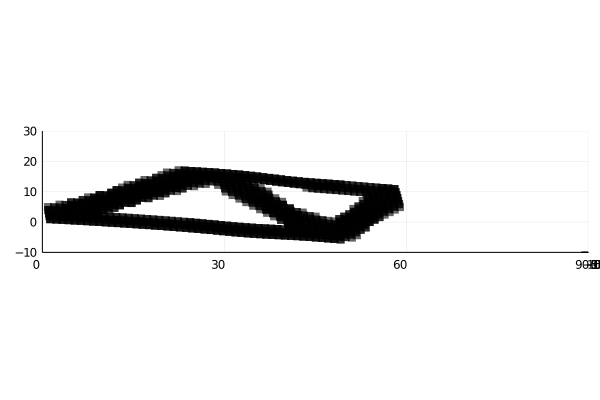
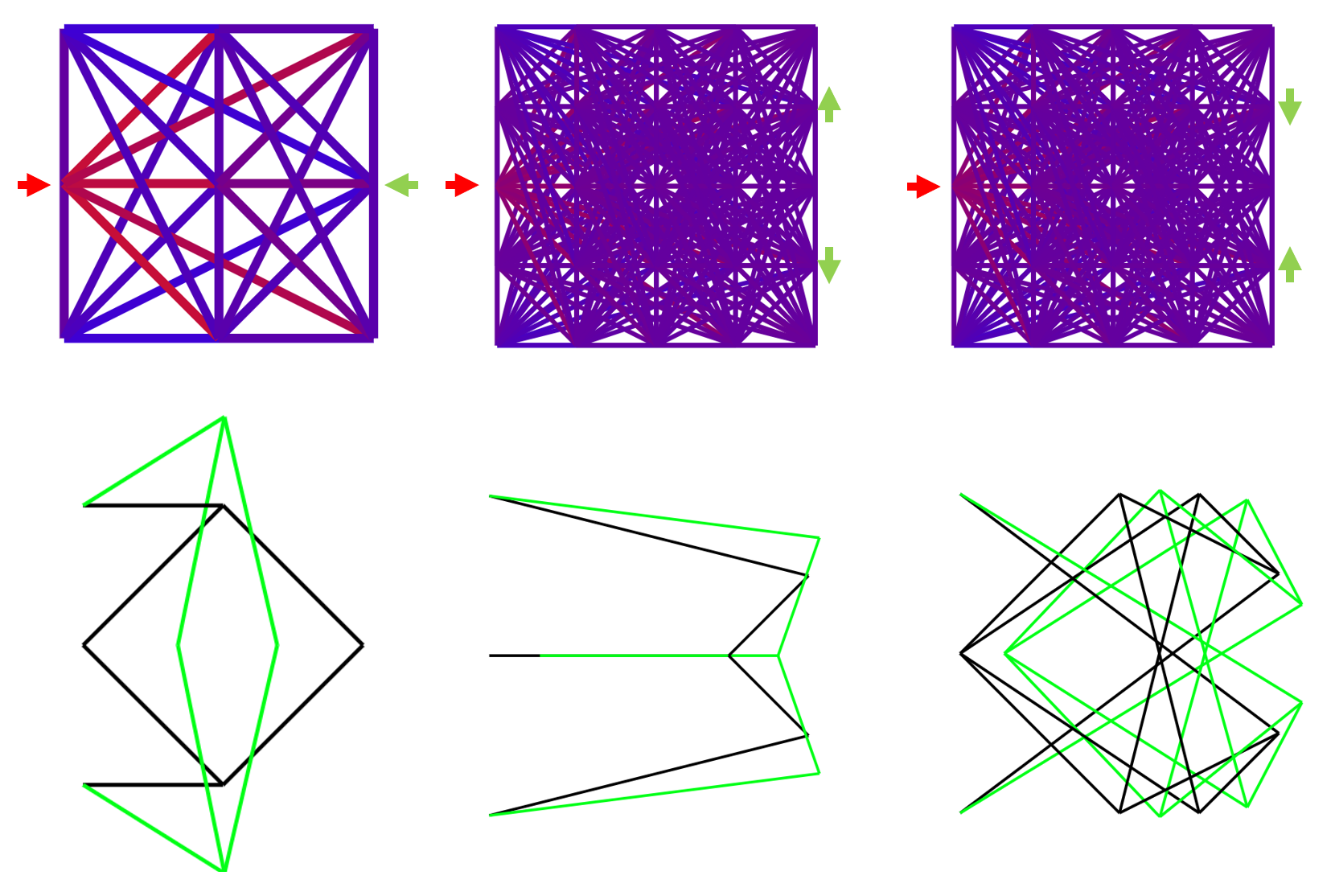
Final Results (Using same cuboct with different densities)
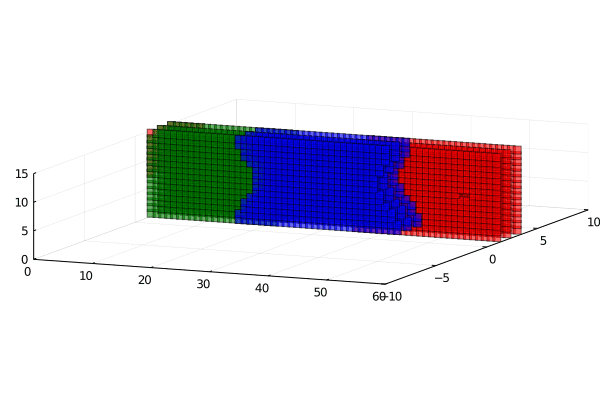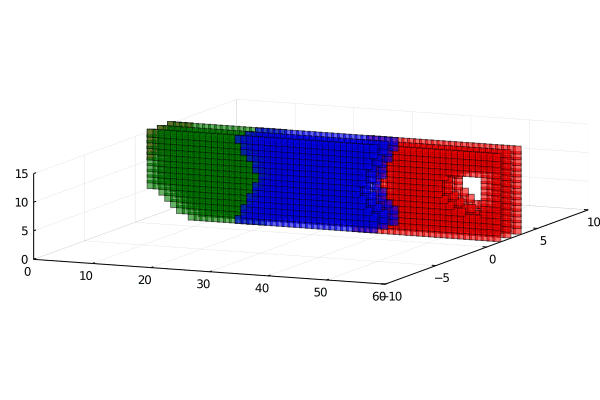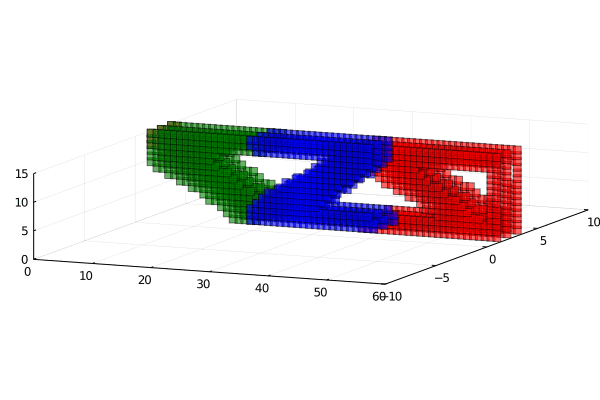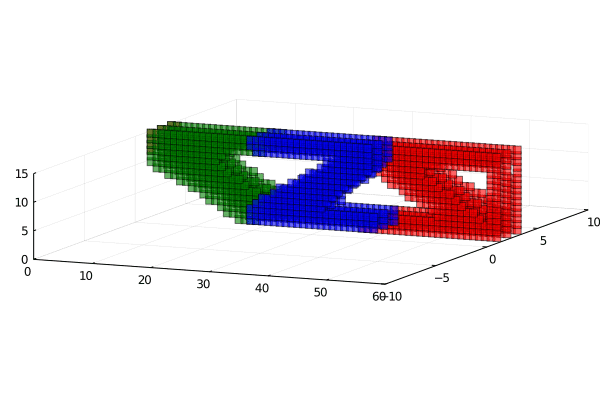
Red more stiff then blue then red.