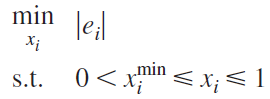Local Opimization: Hybrid Cellular Automata

Approach:

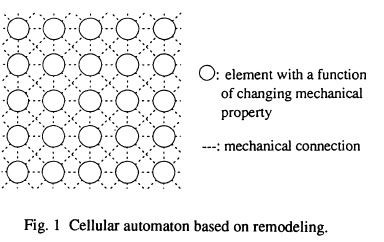
A Cellular Automaton Generating Topological Structures (1994)



Algorithm:

  1. Define cells, load, fixed conditions
  2. calculate local stresses in cells
  3. change material properties of cells based on update rule:

Et+1=Et(1+α(σ/σc−1)E^{t+1}=E^t(1+ \alpha ( \sigma / \sigma_c -1)

  1. Chang cell state ("death", "birth" or "division")
  2. return to step 2



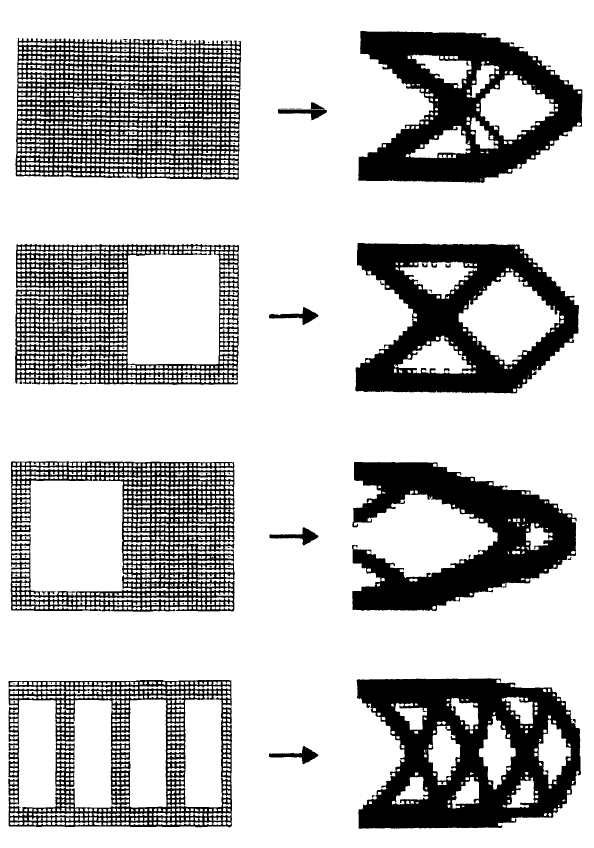
Topology Optimization Using a Hybrid Cellular Automaton Method With Local Control Rules

State αi\alpha_i of each cell is defined by design variables xi(t)x_i(t) (density,geometry,elastic modulus), and field variables Si(t)S_i(t) (stress, stain, strain energy density) (the relation between the amount of energy employed to deform a volume unit of a solid and imposed strain)).

αi={xi(t),Si(t)}\alpha_i = \{x_i{(t)}, S_i(t) \}

Strain Energy defined as follows:

U=∑i=1NUi,viU= \sum_{i=1}^{N}U_i,v_i

UiU_i Strain energy density, viv_i volume

The local minimization problem defined as:



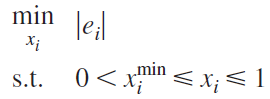
The error signal eie_i:

ei=Uˉi−Ui∗e_i= \bar{U}_i-U^*_i

Ui∗U^*_i is the local SED target,Uˉi\bar{U}_i is the average SED value:

Uˉi=U1+∑j=1NUjN+1\bar{U}_i=\frac{U_1+ \sum_{j=1}^{N}U_j }{N+1}

Neighborhood:

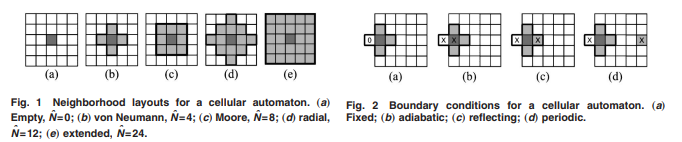
Local Control Rules:

  1. Two position control

    Δxi(t)=cT∗sgn[ei(t)]\Delta x_i(t)=c_T * sgn[e_i(t)]

  2. Proportional control

    Δxi(t)=cp∗ei(t)\Delta x_i(t)=c_p * e_i(t)

  3. Derivative control

    Δxi(t)=cd∗(ei(t)−ei(t−1))\Delta x_i(t)=c_d * (e_i(t)-e_i(t-1))

  4. Integral control

    Δxi(t)=cI∗∑τ=0t(ei(t−τ))\Delta x_i(t)=c_I * \sum_{\tau=0}^{t} (e_i(t-\tau))

Algorithm:

  1. Define design domian, load cases, fixed conditions
  2. Define field variables (Simulation)
  3. calculate error signals
  4. Apply local rules and update the design variables
  5. check for convergence if not return to step 2



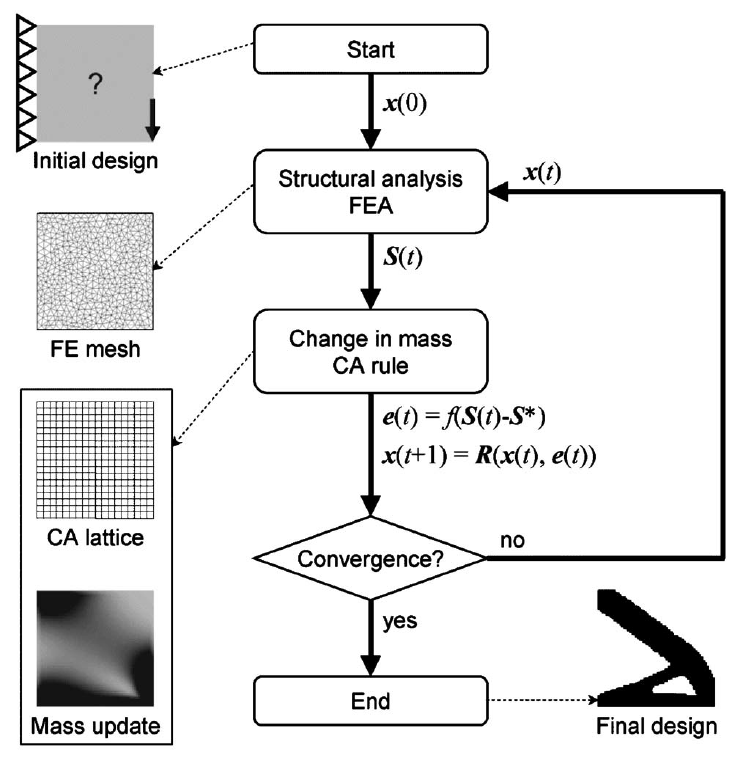
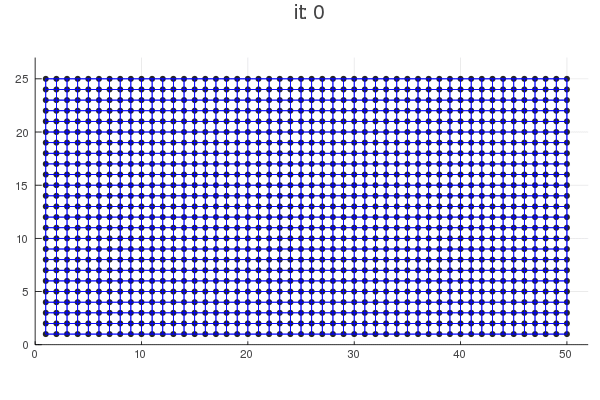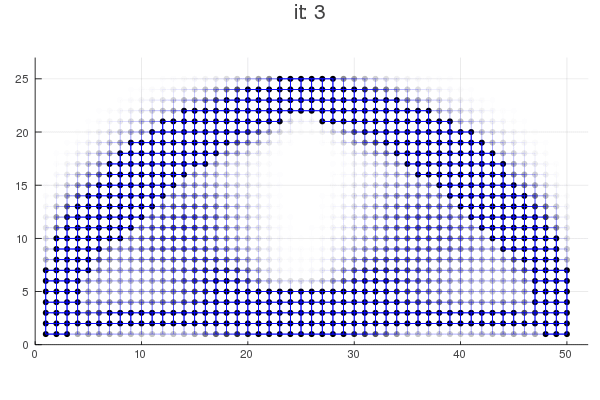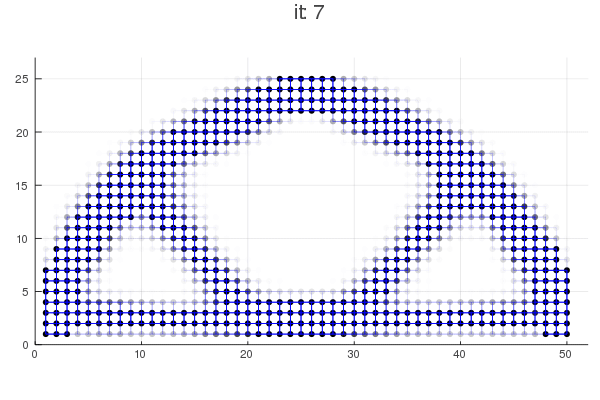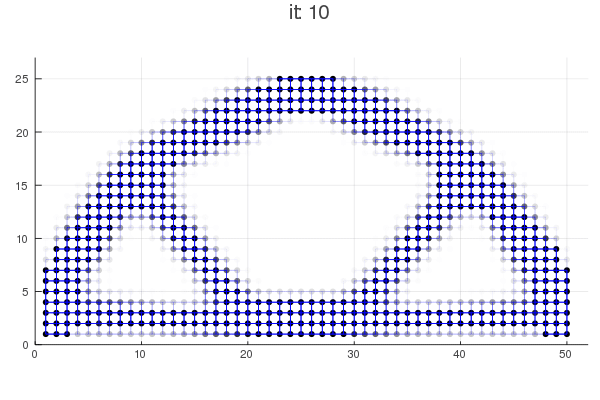
Implementation of HCA

Jupyter Notebook

Next Steps